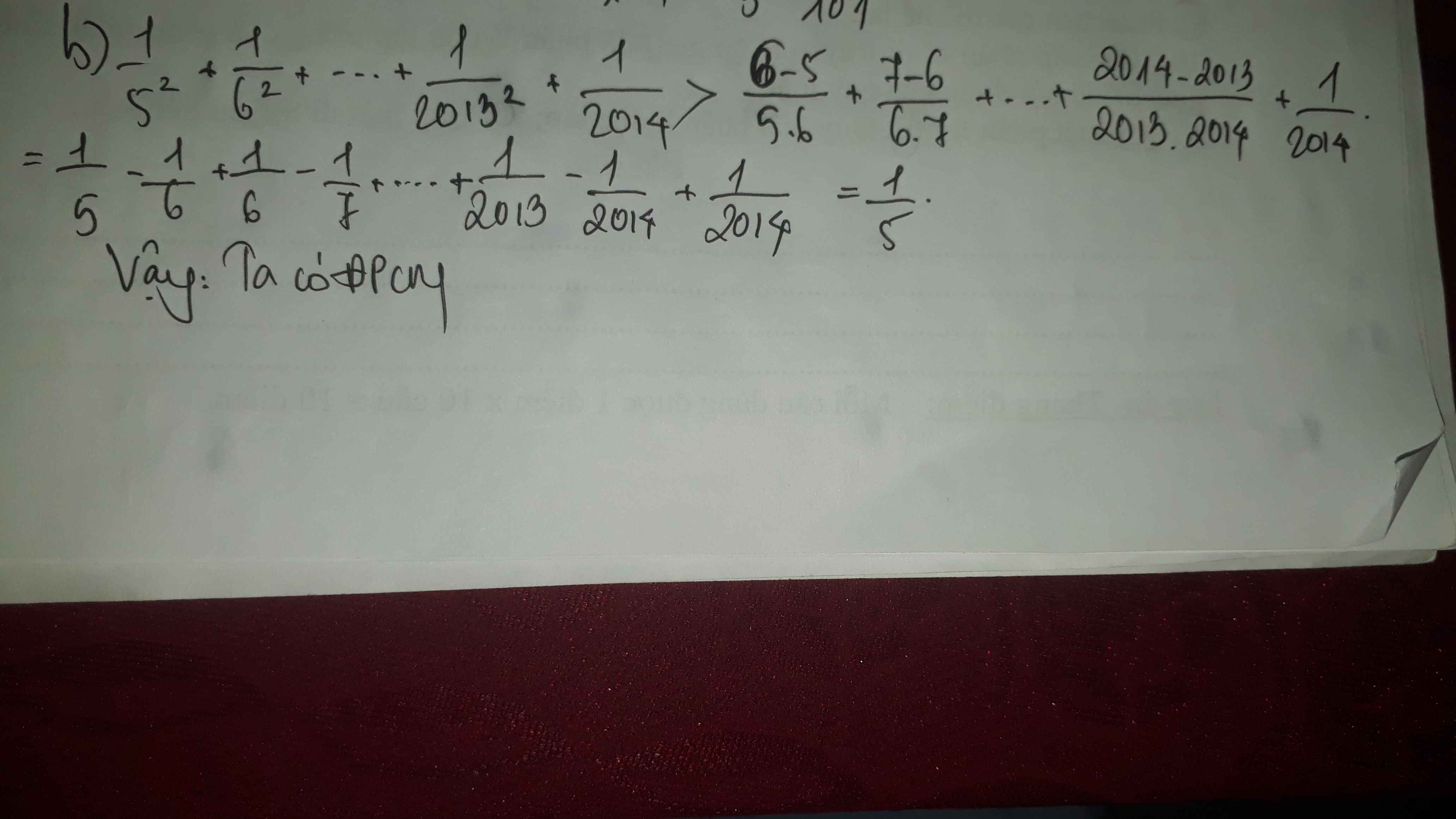25 tháng 7 2021 lúc 11:54
Ôn tập chương III
Các câu hỏi tương tự
25 tháng 7 2021 lúc 14:43
chứng minh rằng :
a) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\) b)\(\dfrac{1}{5^2}+\dfrac{1}{6^5}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
25 tháng 7 2021 lúc 15:02
Chứng minh rằng :
\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014^2}>\dfrac{1}{5}\)
25 tháng 7 2021 lúc 15:39
chứng minh rằng :
b) \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2013^2}+\dfrac{1}{2014}>\dfrac{1}{5}\)
mọi người ơi chú ý hộ mik là cái chỗ \(\dfrac{1}{2014}\) trên kia là đúng nha
a) dfrac{2}{1^2}.dfrac{6}{2^2}.dfrac{12}{3^2}.dfrac{20}{4^2}.dfrac{30}{5^2}.....dfrac{110}{10^2}.x-20
b) left(1+dfrac{1}{2}+dfrac{1}{3}+...+dfrac{1}{2013}right).x+2013dfrac{2014}{1}+dfrac{2015}{2}+...+dfrac{4025}{2012}+dfrac{4026}{2013}
c) left(dfrac{1}{1.2}+dfrac{1}{3.4}+...+dfrac{1}{99.100}right).xdfrac{2012}{51}+dfrac{2012}{52}+...+dfrac{2012}{99}+dfrac{2012}{100}
Đọc tiếp
a) \(\dfrac{2}{1^2}.\dfrac{6}{2^2}.\dfrac{12}{3^2}.\dfrac{20}{4^2}.\dfrac{30}{5^2}.....\dfrac{110}{10^2}.x=-20\)
b) \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2013}\right).x+2013=\dfrac{2014}{1}+\dfrac{2015}{2}+...+\dfrac{4025}{2012}+\dfrac{4026}{2013}\)
c) \(\left(\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right).x=\dfrac{2012}{51}+\dfrac{2012}{52}+...+\dfrac{2012}{99}+\dfrac{2012}{100}\)
Thực hiện phép tính
a) A= \(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)\)\(+\dfrac{1}{4}\left(1+2+3+4\right)+...+\dfrac{1}{2013}\left(1+2+...+2013\right)\)
b) B=\(\dfrac{1-3}{1.3}+\dfrac{2-4}{2.4}+\dfrac{3-5}{3.5}+\dfrac{4-6}{4.6}+...+\dfrac{2011-2013}{2011.2013}+\dfrac{2012-2014}{2012.2014}-\dfrac{2013+2014}{2013.2014}\)
25 tháng 7 2021 lúc 15:00
chứng minh rằng :
\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\)
9 tháng 4 2017 lúc 23:31
Cho: \(A=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+.....+\dfrac{1}{4026}\) và \(B=1+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+....+\dfrac{1}{4025}\) . So sánh: \(\dfrac{A}{B}\) và \(1\dfrac{2013}{2014}\)
1.Tính nhanh:
A dfrac{dfrac{2}{3}-dfrac{1}{4}+dfrac{5}{11}}{dfrac{5}{12}+1-dfrac{7}{11}}
2. Cho: B dfrac{1}{4}+dfrac{1}{5}+dfrac{1}{6}+...+dfrac{1}{19} .Hãy chứng tỏ rằng B 1.
3. Rút gọn:
a) C left(1-dfrac{1}{2}right).left(1-dfrac{1}{3}right).left(1-dfrac{1}{4}right)....left(1-dfrac{1}{20}right)
b) D 1+dfrac{1}{2}+dfrac{1}{2^2}+dfrac{1}{2^3}+...+dfrac{1}{2^{2012}}
4. So sánh: Edfrac{20^{10}+1}{20^{10}-1} và F dfrac{20^{10}-1}{20^{10}-3}
5. Tính giá trị của biểu thức:
M dfrac{dfrac{3}{...
Đọc tiếp
1.Tính nhanh:
A= \(\dfrac{\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{5}{11}}{\dfrac{5}{12}+1-\dfrac{7}{11}}\)
2. Cho: B =\(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{19}\) .Hãy chứng tỏ rằng B > 1.
3. Rút gọn:
a) C= \(\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right)....\left(1-\dfrac{1}{20}\right)\)
b) D= \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2012}}\)
4. So sánh: E=\(\dfrac{20^{10}+1}{20^{10}-1}\) và F =\(\dfrac{20^{10}-1}{20^{10}-3}\)
5. Tính giá trị của biểu thức:
M= \(\dfrac{\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{3}{11}}{\dfrac{4}{5}+\dfrac{4}{7}-\dfrac{4}{11}}\)
Cho: S=\(\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{2018^2}\)chứng tỏ S< \(\dfrac{1}{4}\)