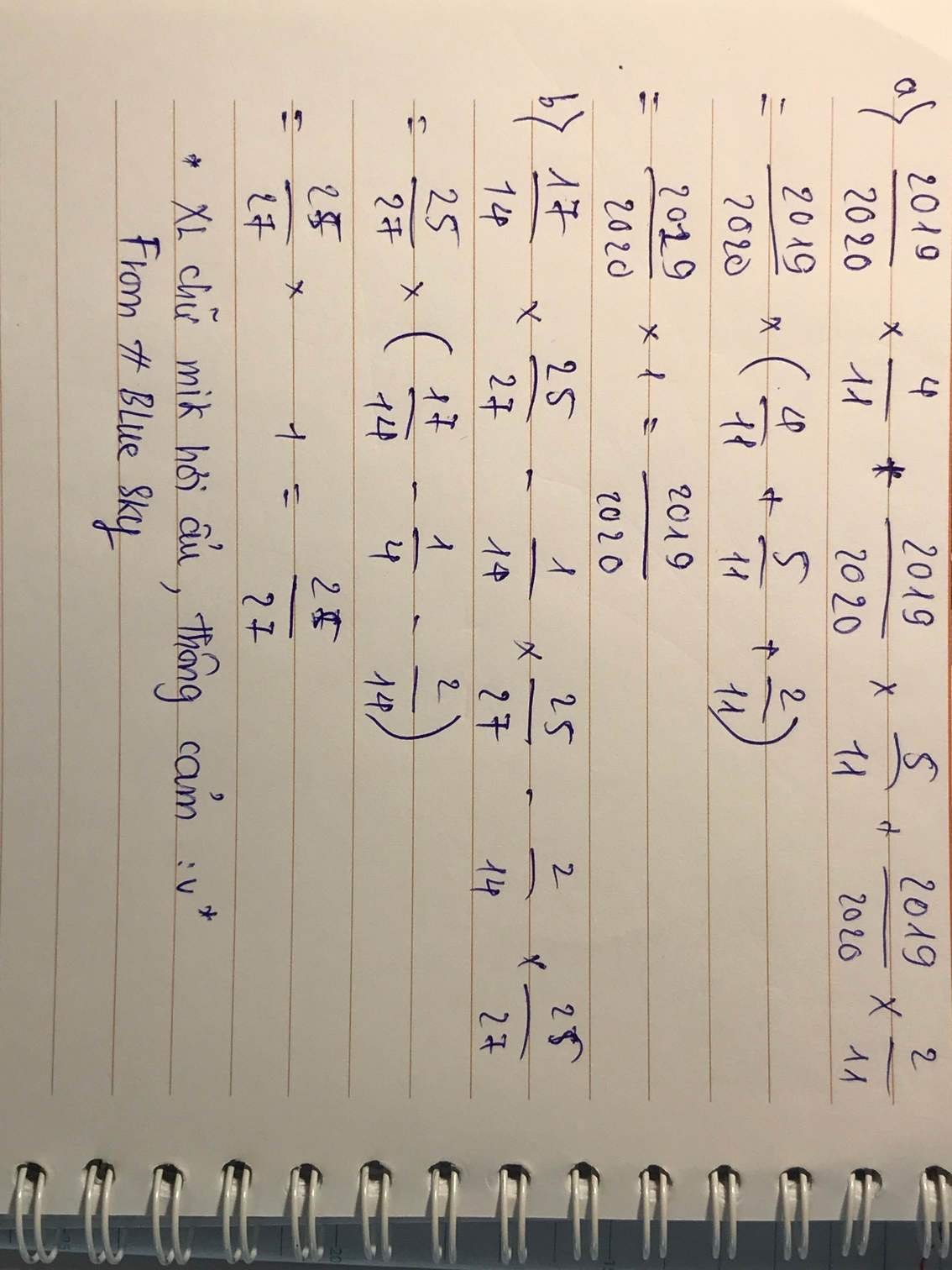\(\left(x-1\right)^2+\left(x-2\right)^2=2\left(x+4\right)^2-\left(22x+27\right)\\ \Rightarrow\left(x^2-2x+1\right)+\left(x^2-4x+4\right)=2\left(x^2+8x+16\right)-\left(22x+27\right)\\ \Rightarrow x^2-2x+1+x^2-4x+4=2x^2+16x+32-22x-27\\ \Rightarrow2x^2-6x+5=2x^2-6x+5\left(luôn.đúng\right)\)

Vậy pt có vô số nghiệm

a) (x + 2)² - 2 (x - 3) = (x + 1)²

<=> x² + 4x + 4 - 2x + 6 = x² + 2x + 1

<=> x² + 2x + 10           = x² + 2x + 1

<=> x² + 2x - x² - 2x       = 1 - 10

<=> 0x                           = -9

Vậy PT vô nghiệm

b) (x + 1)² + (x + 2)²                   = 2 (x + 4)² - (22x + 27)

<=> (x² + 2x + 1) + (x² + 4x + 4) = 2 (x² + 8x + 16) - 22x - 27

<=> x² + 2x + 1 + x² + 4x + 4     = 2x² + 16x + 32 - 22x - 27

<=> 2x² + 6x + 5                        = 2x² - 6x + 5

<=> 2x² + 6x - 2x² + 6x               = 5 - 5

<=> 12x                                     = 0

<=>   x                                       = 0 : 12

<=>   x                                       = 0

Vậy PT có nghiệm x = {0}

\(\sqrt{x^2-6x+9}+\sqrt{x^2-10x+25}+\sqrt{x^2-22x+121}\)

\(=\sqrt{\left(x-3\right)^2}+\sqrt{\left(x-5\right)^2}+\sqrt{\left(x-11\right)^2}\)

\(=\left|x-3\right|+\left|x-5\right|+\left|x-11\right|\)

Đề yêu cầu là gì z pạn?

3 − 2 2 x − 3 = 2 5 + 2 9 − 6 x − 3 2 3 − 2 2 x − 3 = 2 5 − 2 6 x − 9 − 3 2 3 − 2 2 x − 3 = 2 5 + 2 3 2 x − 3 − 3 2 2 3 2 x − 3 − 2 2 x − 3 = 2 5 − 3 2 − 3 2 − 6 3 2 x − 3 = 4 − 15 − 30 10 − 4 3 2 x − 3 = − 41 10 4 3 2 x − 3 = 41 10             4.10 = 41.3. 2 x − 3                 40 = 123. 2 x − 3          2 x − 3 = 40 123                 2 x = 40 123 + 3                 2 x = 40 + 369 123                 2 x = 409 123                    x = 409 246

D=5x²+5x-27x+27/(x)²2(x)(2) +2²

D=5x(x+1)-27(x+1)/(x-2)²

D=(5x-27)(x+1)/(x-20(x-2)

bai cua ban Hakawa Genzo sai roi -27x+27 e thanh -27(x-1) ma 

\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)

Thanks mik chữ cũng hơi ẩu

Lời giải:
Ta có:

\(C=\frac{5(x^2-4x+4)-2x+5}{x^2-4x+4}=\frac{5(x-2)^2-2(x-2)+1}{(x-2)^2}=5-\frac{2}{x-2}+\frac{1}{(x-2)^2}\)

Đặt $\frac{1}{x-2}=t$ thì:

$C=t^2-2t+5=(t-1)^2+4\geq 4$ với mọi $t$

$\Rightarrow C_{\min}=4$. Vậy GTNN của $C$ là $4$. Giá trị này đạt tại $t=1$

$\Leftrightarrow \frac{1}{x-2}=1\Leftrightarrow x=3$