Ta có tam giác ABC = 90 độ nên

góc ABC +góc ACB = 90 độ 

vì lấy điểm E nằm trong tam giác nên 

góc ABE + EBC + ACE + ECB = 90 độ

=> góc EBC + ECB < 90 độ

nên góc BEC > 90 độ

ta có ABC+ACB=90(TC \(\Delta\) vuông)

E\(\in\Delta\) đó \(\Rightarrow\) EBC+ECB<90\(\Rightarrow\) BEC>90 \(\Rightarrow\) BEC tù

tick mình đủ 20 với 

Ta có hình vẽ:

Ta có: ABC + ACB = 90^o

Dễ thấy: EBC < ABC; BCE < ACB

=> EBC + BCE < ABC + ACB = 90^o

Xét Δ BEC có: EBC + BCE + BEC = 180^o (tổng 3 góc của Δ)

Do EBC + BCE < 90^o nên BEC > 90^o

Mà BEC < 180^o => BEC là góc tù (đpcm)

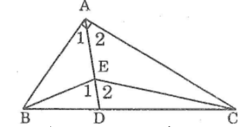
Kéo dài AE cắt BC tại D

Trong ∆ABE ta có ∠E1 là góc ngoài tại đỉnh E

Suy ra: ∠E1 > ∠A1 (tính chất góc ngoài tam giác)(1)

Trong ∆AEC ta có ∠E2 là góc ngoài tại đỉnh E

Suy ra: ∠E2 > ∠A2 (tính chất góc ngoài tam giác)(2)

Cộng từng vế (1) và (2) ta có:

∠E1 + ∠E2 > ∠A1 +∠A2

Hay ∠ (BEC) > ∠ (BAC) = 90º

Vậy góc (BEC) là góc tù.

Ta có tam giác ABC = 90 độ nên

\(\widehat{ABC}+\widehat{ACE}=90^0\) 

Vì lấy điểm E nằm trong tam giác nên\(\widehat{ABE}+\widehat{EBC}+\widehat{ACE}+\widehat{ECB}=90^0\) 

\(\Rightarrow\)\(\widehat{EBC}+\widehat{ECB}< 90^0\); \(\widehat{EBC}+\widehat{ECB}< 90^0\)

Nên \(\widehat{BEC}>90^0\)