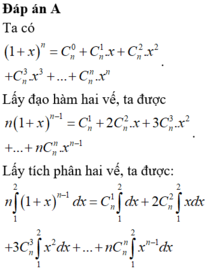32n. 16n= 1024

Những câu hỏi liên quan
Tìm n thuộc N biết
32-n . 16n = 1024
l i m 2 n + 3 2 n + 5 bằng:
A. 5/7
B. 5/2
C. 1
D.+∞
Cho n là số tự nhiên chẵn. CMR: A=20n+16n−3n−1A=20n+16n−3n−1 chia hết cho 323
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Nhận thấy 323=17.19323=17.19 và (17;19)=1(17;19)=1 nên ta cần chứng minh 20n−1+16n−3n20n−1+16n−3n chia hết cho số 1717 và 1919
Ta có
20n−1⋮(20−1)=19;16n−3n⋮(16+3)=1920n−1⋮(20−1)=19;16n−3n⋮(16+3)=19 (vì nn chẵn) (∗)(∗)
Mặt khác
20n+16n−3n−1=20n−3n+16n−120n+16n−3n−1=20n−3n+16n−1
và 20n−3n⋮(20−3)=17;16n−1⋮(16+1)=1720n−3n⋮(20−3)=17;16n−1⋮(16+1)=17 (∗∗)(∗∗)
Từ (∗)(∗∗)(∗)(∗∗) ta suy ra đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên biết: 43.5+85.9+129.15+...+32n.(n+16)=1625
Tìm
n
∈
N
*
sao cho
C
n
1
+
3
C
n
2
+
7
C
n
3
+
.
.
.
+
2
n
-
1
C
n
n...
Đọc tiếp
Tìm n ∈ N * sao cho
C n 1 + 3 C n 2 + 7 C n 3 + . . . + 2 n - 1 C n n = 3 2 n - 2 n - 6480
A. n = 4
B. n = 5
C. n = 6
D. n = 7
Ta có
1 + x n = C n 0 + C n 1 x + C n 2 x 2 + C n 3 x 3 + . . . + C n n x n
Lấy đạo hàm hai vế, ta được
n 1 + x n - 1 = C n 1 + 2 C n 2 x + 3 C n 3 x 2 + . . . + n C n n x n - 1
Lấy tích phân hai vế, ta được:
n ∫ 1 2 1 + x n - 1 d x = C n 1 ∫ 1 2 d x + 2 C n 2 ∫ 1 2 x d x + 3 C n 3 ∫ 1 2 x 2 d x + . . . + n C n n ∫ 1 2 x n - 1 d x
Tính toán các tích phân trên, ta được:
C n 1 + 3 C n 2 + 7 C n 3 + . . . + 2 n - 1 C n n = 3 n - 2 n
Theo đề ta có:
3 n - 2 n = 3 2 n - 2 n - 6480 ⇔ 3 2 n - 3 n - 6480 = 0
Giải phương trình mũ này ta tìm được n = 4. Vậy n = 4 là nghiệm của phương trình đã cho
Đáp án A
Đúng 0
Bình luận (0)
cho thành phần các nguyên tử sau: X(17p,17e,16n) , Y(20p,19,n,20e) , Z(17p,17e,16n) , T(19p,19e,20n). Có bao nhiêu nguyên tố hóa học
z và x có cùng số p trong hạt nhân nên cùng 1 loại ng tố
vậy chỉ có 3 ng tố hh
Đúng 0
Bình luận (0)
so sánh:
a) 536 và 1124
b) 32n và 23n
c) 19920 và 200315
d) 399 và 1121
a) 536 và 1124
Ta có: 536= (53)12=12512 (1)
1124=(112)12=12112 (2)
Từ (1) và (2) => 536>1124
tương tự.....
Đúng 1
Bình luận (0)
Đáp án là :
câu 20 :625 < 1257
câu 21 :536 > 1124
câu 22 :32n < 23n
câu 23 :523 < 6.522
câu 24 :1124 <19920
câu 25 :399 > 112
Đúng 0
Bình luận (1)
a) Ta có: \(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
mà \(125^{12}>121^{12}\left(125>121\right)\)
nên \(5^{36}>11^{24}\)
b) Ta có: \(3^{2n}=\left(3^2\right)^n=9^n\)
\(2^{3n}=\left(2^3\right)^n=8^n\)
mà \(9^n>8^n\left(9>8\right)\)
nên \(3^{2n}>2^{3n}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm
n
∈
ℕ
*
sao cho
C
n
1
+
3
C
n
2
+
7
C
n
3
+
.
.
.
+
(
2
n
-
1
)
C
n
n
3...
Đọc tiếp
Tìm n ∈ ℕ * sao cho
C n 1 + 3 C n 2 + 7 C n 3 + . . . + ( 2 n - 1 ) C n n = 3 2 n - 2 n - 6480 .
A. n=4
B. n=5
C. n=6
D. n=7
Giá trị của biểu thức
P
1
+
3
+
9
+
27
+
...
+
3
2
n
tính theo n là: A.
P
−
1
2
3
2
n
−
1
.
B. ...
Đọc tiếp
Giá trị của biểu thức P = 1 + 3 + 9 + 27 + ... + 3 2 n tính theo n là:
A. P = − 1 2 3 2 n − 1 .
B. P = − 1 2 1 − 3 n .
C. P = − 1 2 3.3 2 n − 1 .
D. P = − 1 2 1 − 3 2 n .
Tìm n∈N để
a) 32n+3 + 4n+11 ⋮ 25
b) 5n - 2n ⋮ 9
c)5n - 24 ⋮63