Các bạn giúp trả lời chi tiết giúp mk với ạ mk cảm ơn

Những câu hỏi liên quan
7 phút 33 giây:3=
giúp mk với ạ mk cần lời giải chi tiết luôn ạ><Cảm ơn
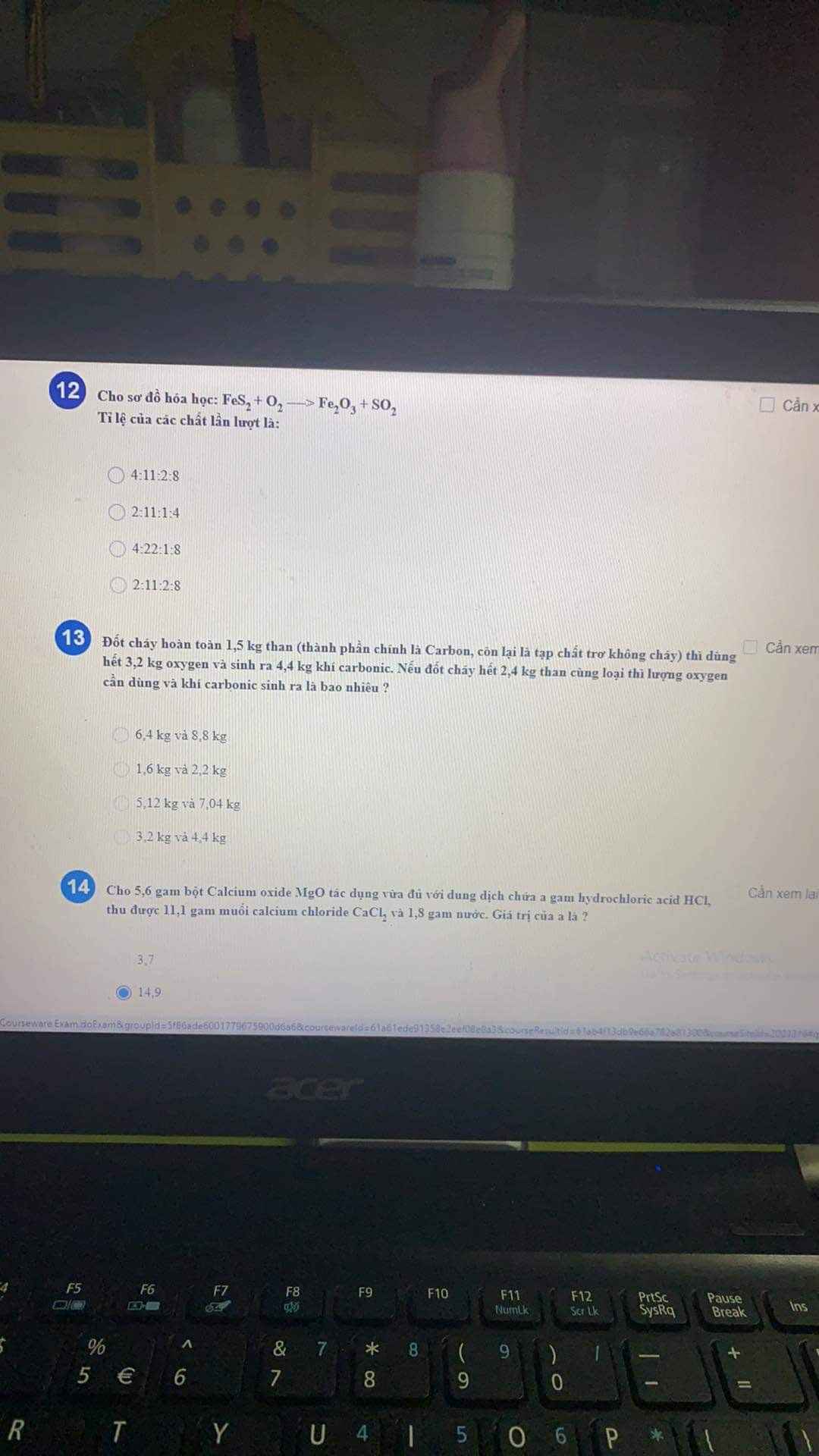
M.n giúp mk câu 13 với ạ, mk cảm ơn rất nhìu(có lời giải chi tiết thì càng tốt nka)
 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
Đúng 0
Bình luận (0)
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Các bạn làm chi tiết giúp mk nhé! Mk cảm ơn!
2:
a: =>x=-3/10+4/5=-3/10+8/10=5/10=1/2
b: =>12,5x=0,25
=>x=1/50
c: =>|x|=1/3+1/4=7/12
=>x=7/12 hoặc x=-7/12
Đúng 0
Bình luận (0)

Các bạn giải chi tiết giúp mk nhé. Mk cảm ơn!
 Mọi người giúp mk giải chi tiết câu này với ạ. Mk cảm ơn
Mọi người giúp mk giải chi tiết câu này với ạ. Mk cảm ơn
\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)
Đúng 1
Bình luận (0)

giúp mk giải chi tiết 4 câu trên ạ
mk cảm ơn
\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
Đúng 0
Bình luận (0)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)
Đúng 0
Bình luận (0)
\(7;\) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}< 2x+\dfrac{1}{2x}-1\left(đk:x>0\right)\)
\(\Leftrightarrow3\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< 2\left(x+\dfrac{1}{4x}\right)-1\left(1\right)\)
\(đặt:\sqrt{x}+\dfrac{1}{2\sqrt{x}}=t>0\)
\(\Leftrightarrow t^2=\sqrt{x}^2+2.\sqrt{x}.\dfrac{1}{2\sqrt{x}}+\left(\dfrac{1}{2\sqrt{x}}\right)^2=x+\dfrac{1}{4x}+1\)
\(\Rightarrow x+\dfrac{1}{4x}=t^2-1\)
\(\left(1\right)\Leftrightarrow3t< 2\left(t^2-1\right)-1\)
\(\Leftrightarrow2t^2-3t-3>0\Leftrightarrow\left[{}\begin{matrix}t< \dfrac{3-\sqrt{33}}{4}\\t>\dfrac{3+\sqrt{33}}{4}\end{matrix}\right.\)
\(\Rightarrow\sqrt{x}+\dfrac{1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\dfrac{2x+1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\sqrt{x}< \dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(2x+1\right)\ge0\\x< \left[\dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\right]^2\\\end{matrix}\right.\)
đến đây dễ dàng rồi như mấy ý trên bạn tự giải quyết để tìm ra x
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho mình xin câu trả lời chi tiết ạ!
Mk cảm ơn trc
Xin lỗi vì đã làm phiền ạ
Gọi khối lượng giấy lớp 7A1 là a
khối lượng giấy lớp 7A2 là b
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{b-a}{4-3}=23\)
Do đó: a=69; b=92
Đúng 1
Bình luận (1)
Giúp mk với mn ơi phần tự luận mn giải chi tiết ra giùm mk ạ cảm ơn mn nhiều 😘😘
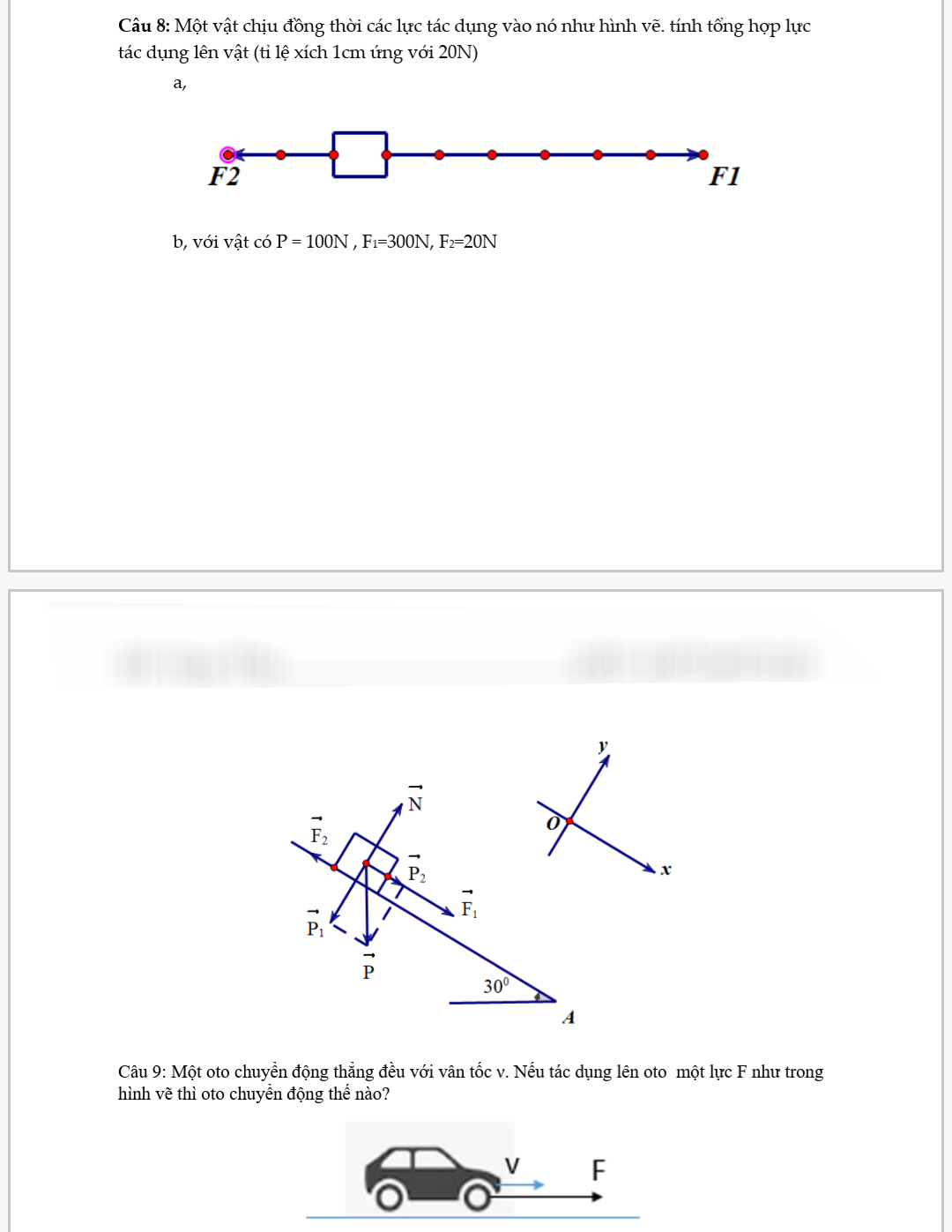

Bạn nên đăng những câu khó nhất hoặc bạn lọc ra những câu tương tự nhau để bản thân có thể vận dụng nhé!
Đúng 1
Bình luận (1)
Giúp mk bài 8 và cho mk xin lời giải chi tiết nhà mk cảm ơn trc
Bài 8:
a: Xét ΔDAB vuông tại B và ΔDAC vuông tại C có
DA chung
AB=AC
Do đó: ΔDAB=ΔDAC
b: Ta có: ΔDAB=ΔDAC
nên DB=DC
hay ΔDBC cân tại D
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
ta có: MB=MC
nên M nằm trên đường trung trực của BC(2)
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,M,D thẳng hàng
Đúng 1
Bình luận (0)



















