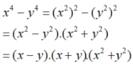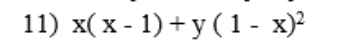
\(=x\left(x-1\right)+y\left(x-1\right)^2=\left(x-1\right)\left[x+y\left(x-1\right)\right]\\ =\left(x-1\right)\left(x+xy-y\right)\)

\(x^4+2008x^2+2007x+2008\\ =x^4-x+2008\left(x^2+x+1\right)=x\left(x^3-1\right)+2008\left(x^2+x+1\right)=x\left(x-1\right)\left(x^2+x+1\right)+2008\left(x^2+x+1\right)\\ =\left(x^2+x+1\right)\left(x^2-x+2008\right)\)

Ta có: \(x^4+2008x^2+2007x+2008\)

\(=x^4-x+2008\left(x^2+x+1\right)\)

\(=x\left(x^3-1\right)+2008\left(x^2+x+1\right)\)

\(=x\left(x-1\right)\left(x^2+x+1\right)+2008\left(x^2+x+1\right)\)

\(=\left(x^2+x+1\right)\left(x^2-x+2008\right)\)

x²-x-12=x²+3x-4x-12=(x²+3x)-(4x+12)=x(x+3)-4(x+3)=(x+3)(x-4)

\(x^2-x-12\)

\(=x^2-x-12\)

\(=\left(x-4\right)\left(x+3\right)\)

64x^4+y^4

=64x^4+16x^2y^2+y^4-16x^2y^2

=(8x^2+y^2)^2-(4xy)^2

=(8x^2-4xy+y^2)(8x^2+4xy+y^2)

x⁴ + x²y² +y⁴                   

= (x²)² +  x²y² + (y²)²          

= (x²)² +  x²y² + (y²)²  + x²y² - x²y²       

= (x²)² +  2 x²y² + (y²)²  - x²y²      

= (x² + y²)²- (xy)²                  

=(x² + y² + xy)(x² + y² - xy)

x³+5x²+3x-9

=x³-x²+6x²-6x+9x-9

=x²(x-1)+6x(x-1)+9(x-1)

=(x-1)(x²+6x+9)

=(x-1)(x+3)²

x^3+5x^2+3x+9 = x^3+6x^2-x^2+9x-6x-9

= x^2(x-1)+6x(x-1)+9(x-1)

= (x-1)(x^2+6x+9) = (x-1)(x+3)^2

Ta có:

x^4-y^4=(x^2-y^2)(x^2+y^2)=(x-y)(x+y)(x^2+y^2)

Lời giải:

a.

$=(x^2)^2+(\frac{1}{2}y^4)^2+2.x^2.\frac{1}{2}y^4-x^2y^4$

$=(x^2+\frac{1}{2}y^4)^2-(xy^2)^2$
$=(x^2+\frac{1}{2}y^4-xy^2)(x^2+\frac{1}{2}y^4+xy^2)$
b.

$=(\frac{1}{2}x^2)^2+(y^4)^2+2.\frac{1}{2}x^2.y^4-x^2y^4$
$=(\frac{1}{2}x^2+y^4)^2-(xy^2)^2$
$=(\frac{1}{2}x^2+y^4-xy^2)(\frac{1}{2}x^2+y^4+xy^2)$

c.

$=(8x^2)^2+(y^2)^2+2.8x^2.y^2-16x^2y^2$

$=(8x^2+y^2)^2-(4xy)^2=(8x^2+y^2-4xy)(8x^2+y^2+4xy)$

d.

$=\frac{64x^4+y^4}{64}=\frac{1}{64}(8x^2+y^2-4xy)(8x^2+y^2+4xy)$

c: \(64x^4+y^4\)

\(=64x^4+16x^2y^2+y^4-16x^2y^2\)

\(=\left(8x^2+y^2\right)^2-\left(4xy\right)^2\)

\(=\left(8x^2+y^2-4xy\right)\left(8x^2+y^2+4xy\right)\)