+1 còn tùy vào từng loại cần tìm nếu đơn giản là đa thức bậc 2 thì sử dụng máy tính hoặc cứ tìm thôi ;-;

+2 Vì \(m^2+3\ge3\) thì để dấu = xảy ra tức là : \(m^2+3=3\) \(\Leftrightarrow m^2=0\)

<=> m = 0 .

ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)

Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)

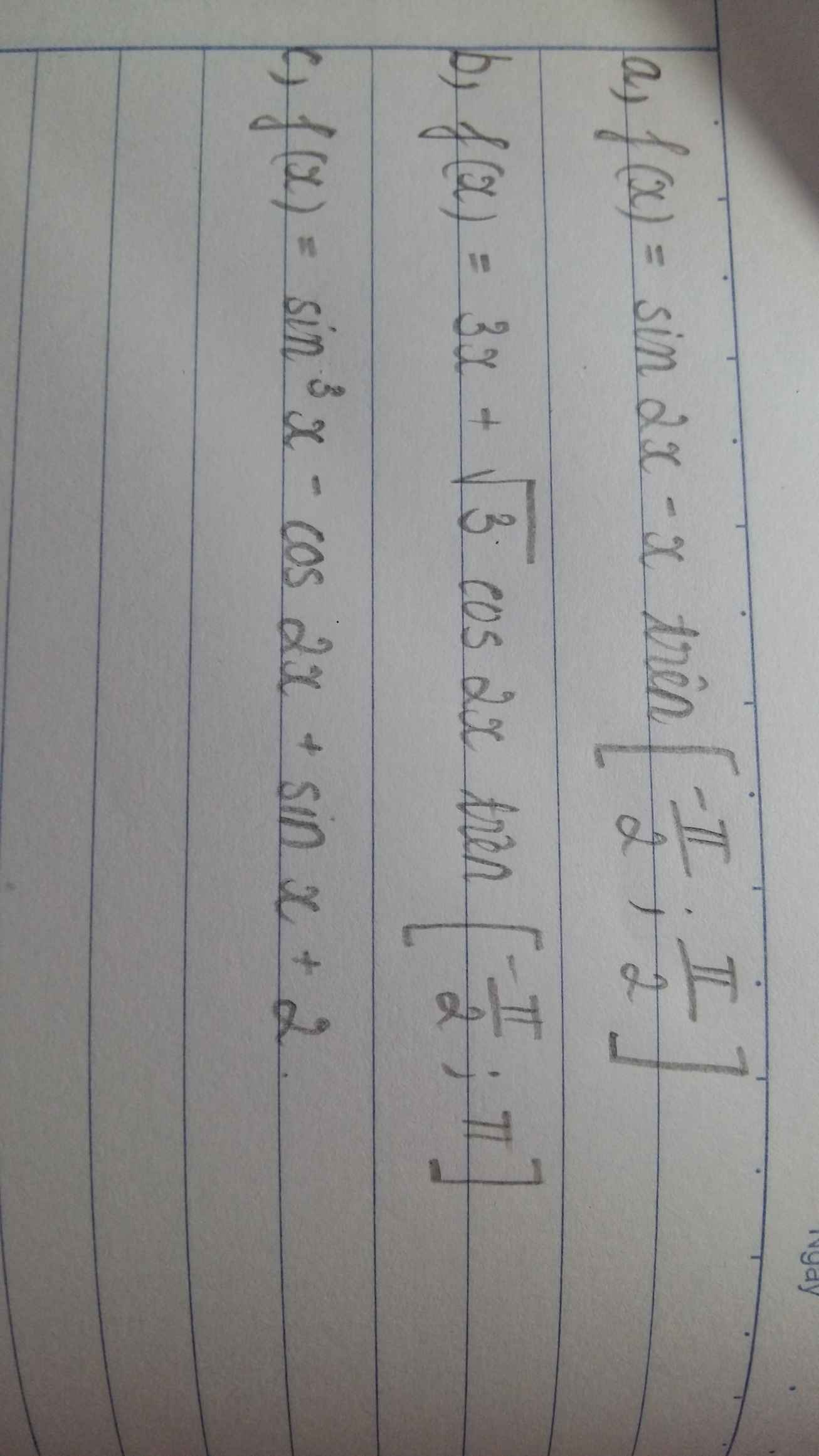
a.

\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)

\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)

Ta có:

\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)

\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)

\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)

\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)

So sánh các giá trị trên ta được:

\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)

\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)

b.

\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)

\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)

Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)

\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)

\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)

\(f\left(\pi\right)=3\pi+\sqrt{3}\)

Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)

\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)

c.

\(f\left(x\right)=sin^3x-\left(1-2sin^2x\right)+sinx+2=sin^3x+2sin^2x+sinx+1\)

Đặt \(sinx=t\Rightarrow t\in\left[-1;1\right]\)

Xét hàm \(f\left(t\right)=t^3+2t^2+t+1\) trên \(\left[-1;1\right]\)

\(f'\left(t\right)=3t^2+4t+1=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{3}\end{matrix}\right.\)

\(f\left(-1\right)=1\) ; \(f\left(-\dfrac{1}{3}\right)=\dfrac{23}{27}\) ; \(f\left(1\right)=5\)

\(\Rightarrow f_{max}=5\) ; \(f_{min}=\dfrac{23}{27}\)

tìm GTLN thì đưa về dạng A^2 - k hoặc /A/ -k

GTNN đưa về dạng A^2 + k hoặc /A/ +k

Choi mình VD đi bạn

tìm GTLN của  x^2 - 5

Tìm GTLN của x^2 +1

đấy là các dạng cơ bản. tuy nhiên khi làm , đề bài có thể lắt léo hơn nhưng về cơ bản cuối cùng phải dưa đc về dạng như tui đã bảo

Ta có :

|x - 1/2| > 0

Vậy GTNN của |x - 1/2| = 0 <=> x - 1/2 = 0 <=> x = 1/2