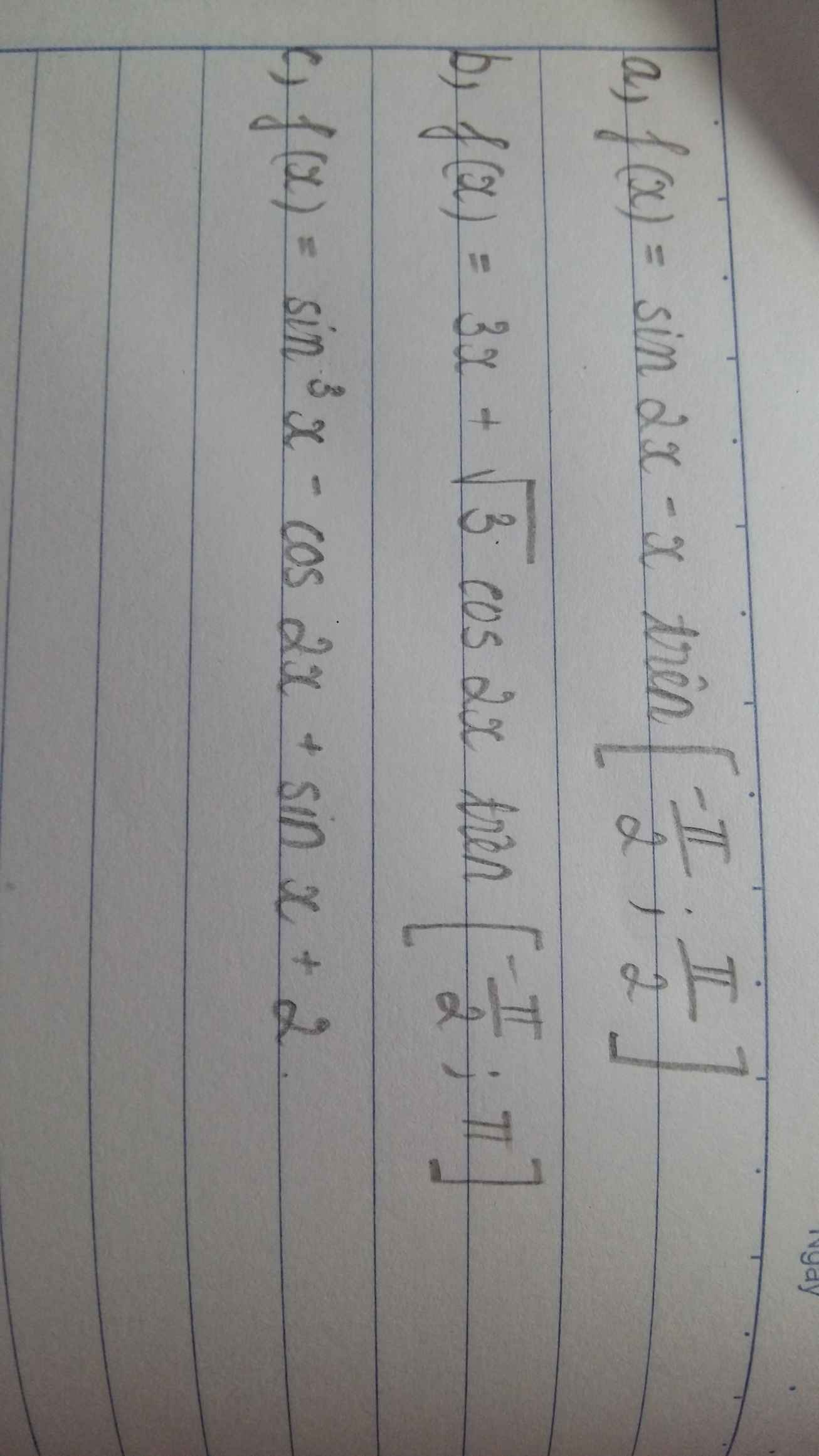a.
\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)
Ta có:
\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)
\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)
So sánh các giá trị trên ta được:
\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)
\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)
b.
\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)
\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)
\(f\left(\pi\right)=3\pi+\sqrt{3}\)
Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)
c.
\(f\left(x\right)=sin^3x-\left(1-2sin^2x\right)+sinx+2=sin^3x+2sin^2x+sinx+1\)
Đặt \(sinx=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(f\left(t\right)=t^3+2t^2+t+1\) trên \(\left[-1;1\right]\)
\(f'\left(t\right)=3t^2+4t+1=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{3}\end{matrix}\right.\)
\(f\left(-1\right)=1\) ; \(f\left(-\dfrac{1}{3}\right)=\dfrac{23}{27}\) ; \(f\left(1\right)=5\)
\(\Rightarrow f_{max}=5\) ; \(f_{min}=\dfrac{23}{27}\)