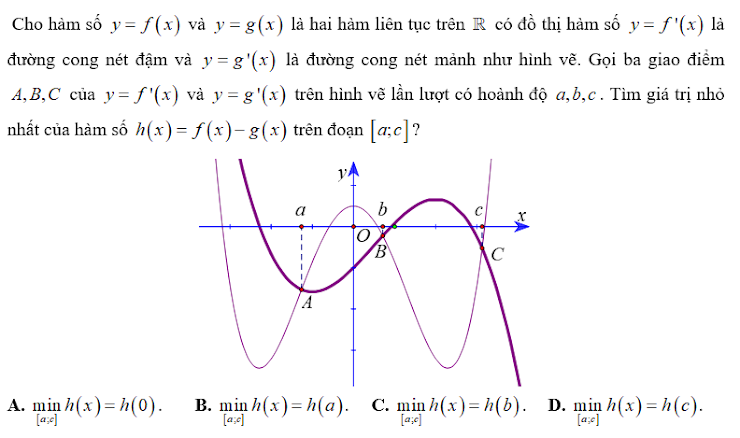
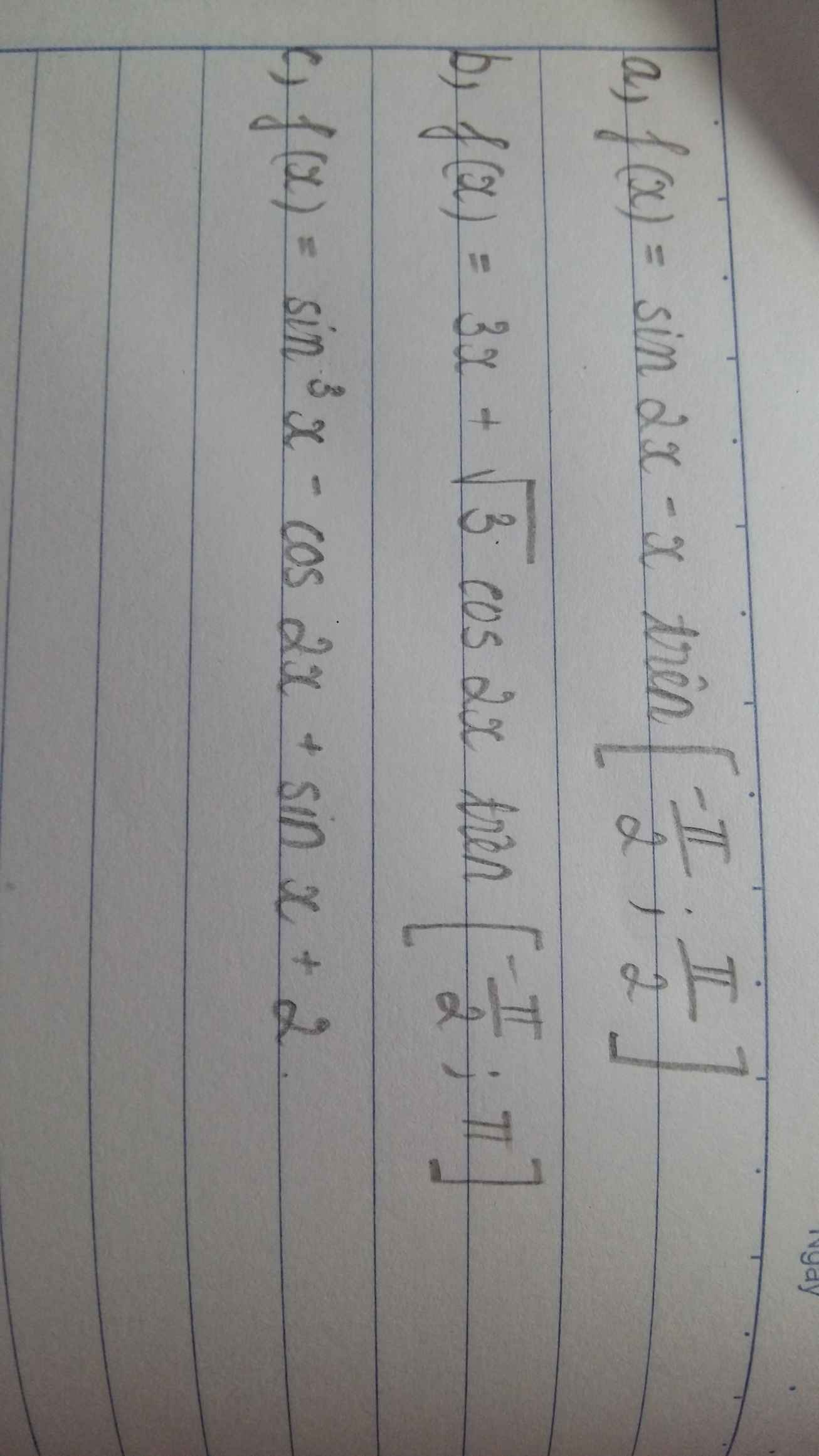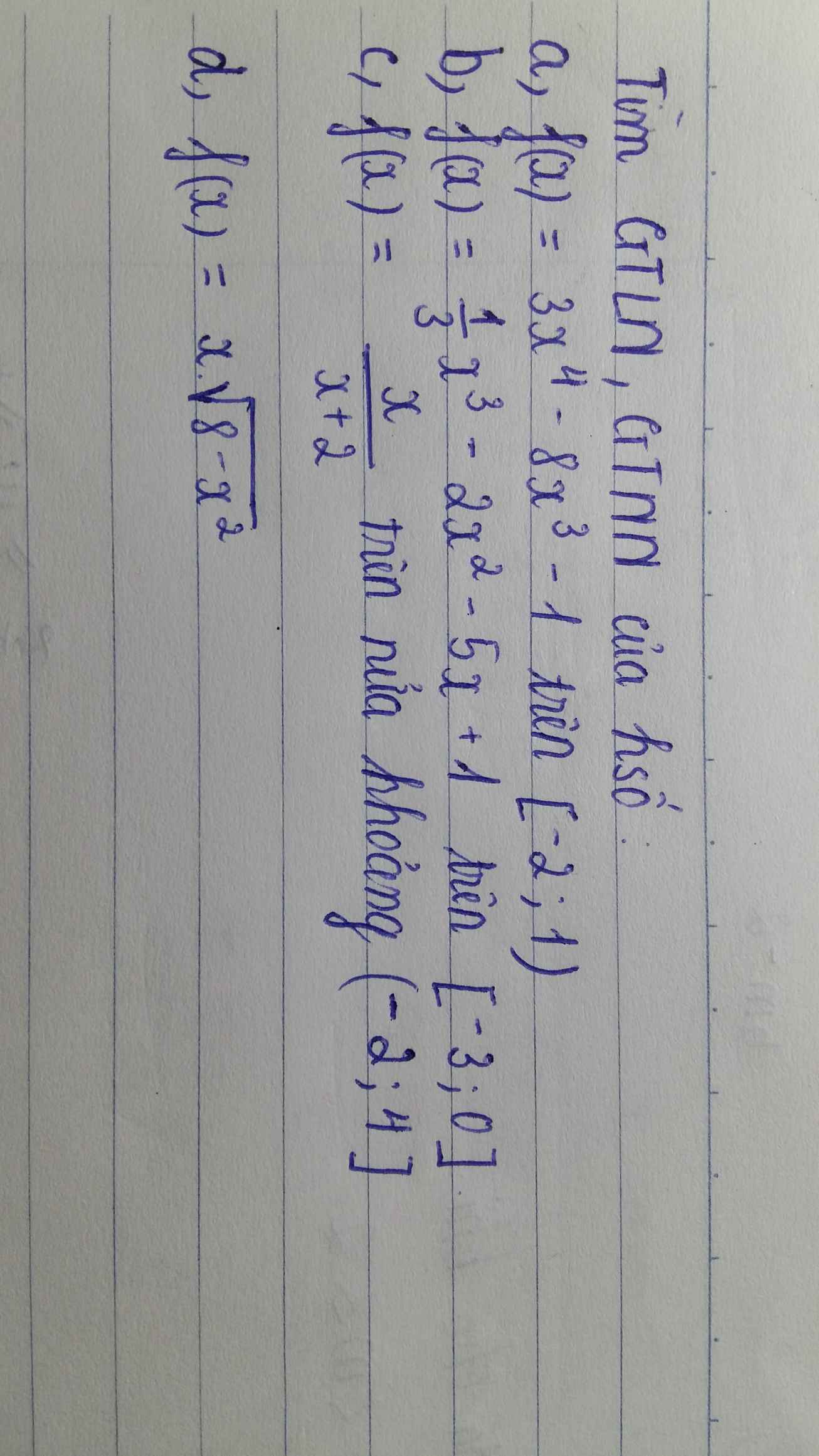\(f'\left(x\right)=-3x^2+m\)
TH1: \(m\le0\Rightarrow f\left(x\right)\) nghịch biến trên R
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(1\right)=m-7=10\Rightarrow m=17>0\left(ktm\right)\)
TH2: \(m>0\Rightarrow\) hàm có 2 điểm cực trị \(x=\pm\sqrt{\dfrac{m}{3}}\) \(\Rightarrow\) hàm nghịch biến trên \(\left(\dfrac{\sqrt{m}}{3};+\infty\right)\) và đồng biến trên \(\left(-\sqrt{\dfrac{m}{3}};\sqrt{\dfrac{m}{3}}\right)\)
- Nếu \(\sqrt{\dfrac{m}{3}}\ge3\Rightarrow m\ge27\Rightarrow\) hàm đồng biến trên \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(3\right)=3m-33=10\Rightarrow m=\dfrac{40}{3}< 27\left(ktm\right)\)
- Nếu \(\sqrt{\dfrac{m}{3}}\le1\Rightarrow m\le3\Rightarrow\) hàm nghịch biến trên \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(1\right)=m-7=10\Rightarrow m=17>3\left(ktm\right)\)
- Nếu \(1< \sqrt{\dfrac{m}{3}}< 3\Rightarrow3< m< 27\) \(\Rightarrow x=\sqrt{\dfrac{m}{3}}\) là điểm cực đại và là cực trị duy nhất thuộc \(\left[1;3\right]\)
\(\Rightarrow\max\limits_{\left[1;3\right]}f\left(x\right)=f\left(\sqrt{\dfrac{m}{3}}\right)=-\dfrac{m}{3}\sqrt{\dfrac{m}{3}}+m\sqrt{\dfrac{m}{3}}-6=10\)
\(\Rightarrow m=12\) (thỏa mãn)
\(\Rightarrow m-x_0=12-\sqrt{\dfrac{12}{3}}=10\)