cho tam giác ABC đường cao AH , H thuộc AC chứng minh
a, Tính BC và AH
b, gọi M và N lần lượt là hình chiếu của H trên AB và AC . Hỏi tứ giác AMNH lag hình gì?
c, tính MN
d, cminh:tam giác AMN đồng dạng với tam giác ABC
cho tam giác vuông ABC vuông ở A ; có AB = 8cm ; AC = 15cm ; đường cao AH
a) tính BC ; BH ; AH
b) gọi m,n lần lượt là hình chiếu của H lên AB và AC . tứ giác AMNH là hình gì ? tính độ dài đoạn MN
c) chứng minh AM.AB=AN.AC
Cho tam giác ABC vuông tại A có AB=8cm AC=15cm Kẻ đường cao AH
a) CM 🔺️AHB và 🔺️CAB đồng dạng. Tính AB
b) Gọi M,N lần lượt là hình chiếu của H trên AB,AC. Tứ giác AMNH là hình gì? Tính độ dài MN
c) CM AM.AB=AN.AC
Cho tam giác vuông ABC vuông ở A ;có AB = 8cm ; AC =15cm ; đường caoAH.
a) Tính BC ; BH;AH
b)Gọi M,N lần lượt là hình chiếu của H lên AB và AC . Tứ giác AMNH là hình gì? Tính độ dài đoạn MN.
c) Chứng minh : AM.AB=AN.AC
a) XétΔABC vg tại A
⇒ BC²=AB²+AC²
⇒ BC=17cm
Xét ΔABH và ΔCBA có:
góc AHB= góc CBA
góc B: chung
⇒ ΔABH ∞ ΔCBA (g.g)
⇒ AB/BC=BH/BA
⇒ BH=AB²/BC
⇒ BH=64/17
Xét ΔABH vg tại H
⇒AB²=BH²+AH²
⇒ AH=120/17
b) xét tg AMHN có: góc AMH= góc ANH= góc MAN=90
⇒ tg AMHN là hcn (dhnb)
⇒ AH=MN (t/c hcn)
⇒ MN=120/17
, Ta thấy tam giác AMH đồng dạng tam giác AHB (g.g) suy ra AM/AH = AH/ AB => AM.AB =AH^2
tam giác ANH đồng dạng tam giác AHC (g.g)
=> AN/AH = AH/AC
=> AN.AC = AH^2
suy ra AM.AB = AN.AC.
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC vuông ở A ; có AB = 8cm ; AC = 15cm ; đường cao AH
a] Tính BC , BH , AH
b] Gọi M, N lần lượt là hình chiếu của H lên AB và AC . Tứ giác AMNH là hình gì ?
c] chứng minh AM. AB = AN.AC
Ý a của bạn nhé còn ý b và c mjnh gửi sau
Gửi bạn ý b nhé còn ý c
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ? A.
S
A
⊥
A
B
C
B.
O
∈
S
H
C.
S
A
H
⊥...
Đọc tiếp
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
A. S A ⊥ A B C
B. O ∈ S H
C. S A H ⊥ S B C
D. S B C , A B C ^ = S B A ^
Chọn D.
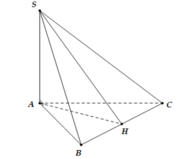
+) Ta có :
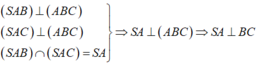
⇒ Suy ra : A đúng.
+) Ta có :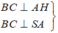 
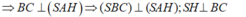
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
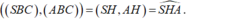
⇒ Suy ra : D sai.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC
a.AM.AB=AN.AC
b.Chứng minh tam giác AMN đồng dạng tam giác ACB
Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$AM.AB=AH^2$
$AN.AC=AH^2$
$\Rightarrow AM.AB=AN.AC$ (đpcm)
b.
Vì $AM.AB=AN.AC\Rightarrow \frac{AM}{AN}=\frac{AC}{AB}$
Xét tam giác $AMN$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AM}{AN}=\frac{AC}{AB}$ (cmt)
$\Rightarrow \triangle AMN\sim \triangle ACB$ (c.g.c)
Ta có đpcm.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH=4cm, CH=9cm. Gọi I và K lần lượt là hình chiếu của H lên AB và AC a. Chứng minh tứ giác AIHK là hình chữ nhật b. Cm tam giác AKI đồng dạng với tam giác ABC c. Tính diện tích của tam giác ABC
a: góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hcn
b: AIHK là hcn
=>góc AIK=góc AHK=góc C
=>ΔAIK đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,đường cao AH. Gọi M,N lần lượt là hình chiếu vuông góc của H lên AB và AC. a, biết AC bằng 16 cm, sinCAH=4/5. Tính độ dài các cạnh BC,AB và cosB b,chứng minh AM x AB = AN x AC và tam giác ABC đồng dạng với tam giác AMN. c, chứng minh MA x MB + NA × NC=HB×HC d, Chứng minh S AMN/ S ABC=sin²B×sin²C
b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, AC vuông góc với mặt phẳng (ABC), AH là đường cao trong tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng định sai? A.
A
H
⊥
A
C
B.
A
H
⊥
B
C
C.
S
A
⊥
B
C
D.
A
H
⊥
S
C
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, AC vuông góc với mặt phẳng (ABC), AH là đường cao trong tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. A H ⊥ A C
B. A H ⊥ B C
C. S A ⊥ B C
D. A H ⊥ S C
