cho tam giác abc(Â=90) AB=9CM, AC=12CM.BE LÀ TIAN PHÂN GIÁC CỦA GÓC B(E THUỘC AC) TỪ E KẺ EH VƯƠNG GÓC VỚI BC.
a) tính BC
b) chứng minh tam giác ABE=tam giác HBE
,c )chứng minh BE là đường trung trực của AH
Cho tam giác ABC vuông tại A,đường phân giác BE(E thuộc AC)Kẻ EH vuông góc BC(H thuộc BC)
a)Tính góc BAC
b)Chứng minh góc ABE=góc CBE và tam giác ABE=tam giác HBE
c)Chứng minh BE là đường trung trực của AH
d)Kẻ đường cao AK của tam giác ABC.Chứng minh AB+AC<BC+2AK
e)Tia HE cắt tia BA tại M.Chứng minh BE vuông góc MC
Giúp mình với mọi người
cho tam giác ABC có A=90 độ, BE là đường phân giác của B cắt cạnh AC tại E (E thuộc AC) kẻ EH vuông góc với BC (H thuộc BC)
a) chứng minh tam giác ABE=tam giác HBE và AE=EH
b)chứng minh BE là đường trung trực của AH
c)chung minh AE<EC
Cho tam giác ABC vuông tại A. Đường phân giác góc ABC cắt AC ở E. Kẻ EH vuông góc với BC {H thuộc BC}.Đường thẳng HE cắt AB ở K
a,Chứng minh tam giác ABE = tam giác HBE đó suy ra BE là Đường trung trực của AH
b,Chứng minh BE vuông góc với CK
a, xét tam giác ABE và tam giác HBE có : BE chung
góc ABE = góc HBE do BE là phân giác
góc BAE = góc BHE = 90
=> tam giác ABE = tam giác HBE (ch - gn)
cho tam giác ABC vuông tại A có đường phân giác BE {E thuộc AC}. kẻ EH vuông BC
+ TÍNH góc BAC
+ góc ABE = góc CBE
+Chúng minh BE là đường trung trực của AH
+Gọi AK là đường cao của tam giác ABC
chứng minh AB+AC< BC+AK
Cho tam giác ABC vuông tại A .Đường phân giác của góc B cắt AC tại E.Kẻ EH vuông góc với BC (H thuộc BC) . a/ Chứng minh tam giác ABE = tam giác HBE b/ Chứng minh BE là đường trung trực của đoạn thẳng AH. c/ Gọi I là giao điểm của Be và AH .Cho AB = 10 cm, AH = 16 cm và G là trọng tâm của tam giác ABH. Tính BG. d/ Gọi K là giao điểm của AB và EH. Chứng minh tam giác BCK cân.
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: ta có: ΔABE=ΔHBE
nên AE=HE; BA=BH
Suy ra: BE là đường trung trực của AH
Cho tam giác ABC vuông tại A phân giác của góc B cắt AC tại E Vẽ EH vuông góc với BC gọi K là giao điểm của AB và EH chứng minh a,tam giác ABE=tam giác HBE b: BE là trung trực của AH c: EK = EC d: Tam giác BKC là tam giác cân
a) Vì EH ⊥ BC ( gt )
⇒ △ BHE vuông tại H
Xét tam giác vuông BAE và tam giác vuông BHE có :
BE chung
\(\widehat{B_1}=\widehat{B_2}\) ( BE là tia phân giác của \(\widehat{BAC}\))
⇒ △ BAE = △ BHE ( cạnh huyền - góc nhọn )
b) Gọi I là giao điểm của AH và BE
Xét △ ABI và △ HBI có :
BA = BH [ △ BAE = △ BHE (cmt) ]
\(\widehat{B_1}=\widehat{B_2}\) ( BE là tia phân giác của \(\widehat{BAC}\) )
BI chung
⇒ Δ ABI = Δ HBI ( c.g.c )
⇒ \(\widehat{AIB}=\widehat{AIH}\) ( 2 góc tương ứng )
Mà \(\widehat{AIB}+\widehat{AIH}\) = 1800 ( 2 góc kề bù )
⇒ \(\widehat{AIB}=\widehat{AIH}\) = 900
⇒ BI ⊥ AH (1)
Ta có: IA = IH ( Δ ABI = Δ HBI ( cmt )
Mà I nằm giữa hai điểm A và H (2)
⇒ I là trung điểm của AH ( 3)
Từ (1) (2) (3) ⇒ BI là trung trực của AH
Hay BE là trung trực của AH
c) Xét Δ KAE và Δ CHE có:
\(\widehat{KAE}=\widehat{CHE}\) ( = 900 )
AE = HE ( Δ BAE = Δ BHE (cmt)
\(\widehat{AEK}=\widehat{HEC}\) ( 2 góc đối đỉnh )
⇒ Δ KAE = Δ CHE ( g.c.g )
⇒ EK = EC ( 2 cạnh tương ứng )
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Ta có: ΔBAE=ΔBHE
nên BA=BH và EA=EH
hay BE là đường trung trực của AH
c: Xét ΔEKA vuông tại A và ΔECH vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔEKA=ΔECH
Suy ra: EK=EC và AK=HC
d: Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
Xét ΔBKC có BK=BC
nên ΔBKC cân tại B
Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E.
kẻ EH vuông góc với BC tại H (H thuộc BC ). chứng minh :
a) tam giác ABE = tam giác HBE
b) BE là đường trung trực của đoạn thẳng AH
c) EC > AE
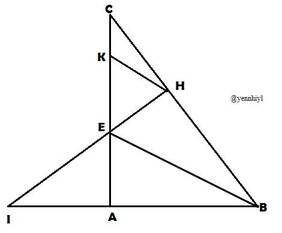
Cho tam giác ABC vuông ở A có góc B bằng 60 độ . Tia phân giác của góc ABC cắt AC ở E. Kẻ EH vuông góc với BC
a) Chứng minh tam giác ABE bằng tam giác HBE
b) Chứng minh HB = HC
c) Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh tam giác EHK đều
d) Gọi I là giao điểm của BA và HE. Chứng minh IE > EH
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
cho tam giác ABC có góc A =90 độ .tia phân giác của góc ABC cắt AC tại E .qua E kẻ EH vuông góc với BC (H thuộc BC)
1,chứng minh tam giác ABE=HBE
2,chứng minh BE là đường trung trực của AH
3,chứng minh EA <EC
4,gọi K là giao điểm của AB và HE .chứng minh BE vuông góc với CK ;AH song song với CK
giúp mk vs ạ.mk đg cần gấp