Hi bạn, câu 29 này mình có cái cách này dùng cho các bài lim khi rơi vào trường hợp vô định thì bạn dùng quy tắc L'Hospital làm cho nhanh với trường hợp các bài trắc nghiệm như thế này

Ở bài 29 này đang rơi vào dạng \(\dfrac{0}{0}\) nên dùng quy tắc L'Hospital được nè. Bạn làm như sau:

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\x\ge-3\end{matrix}\right.\)

Bước 1: Đạo hàm tử mẫu, ta được: \(\dfrac{\dfrac{1}{2}\left(x+3\right)^{-\dfrac{1}{2}}}{1}\)

Bước 2: Thay điểm cần tính giới hạn: (x=1)

ta sẽ được \(\dfrac{1}{4}\)

Vậy \(lim_{x\rightarrow1}\dfrac{\sqrt{x+3}-2}{x-1}=\dfrac{1}{4}\)

\(\Rightarrow a=1;b=4\)

Vậy S=4a-b=0

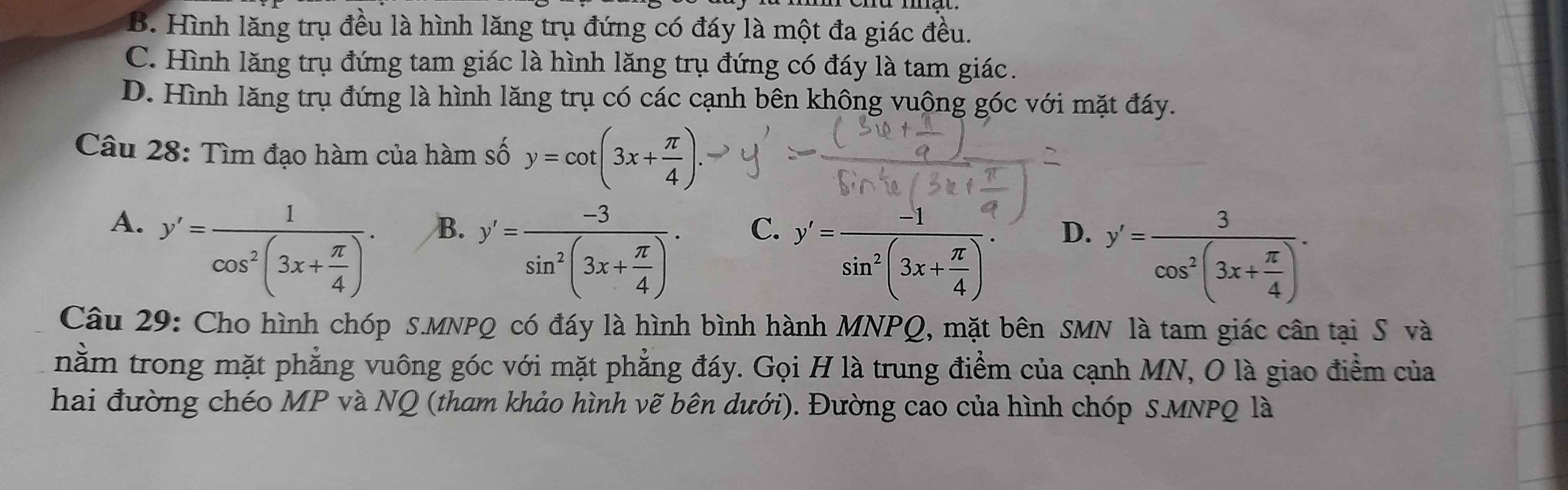
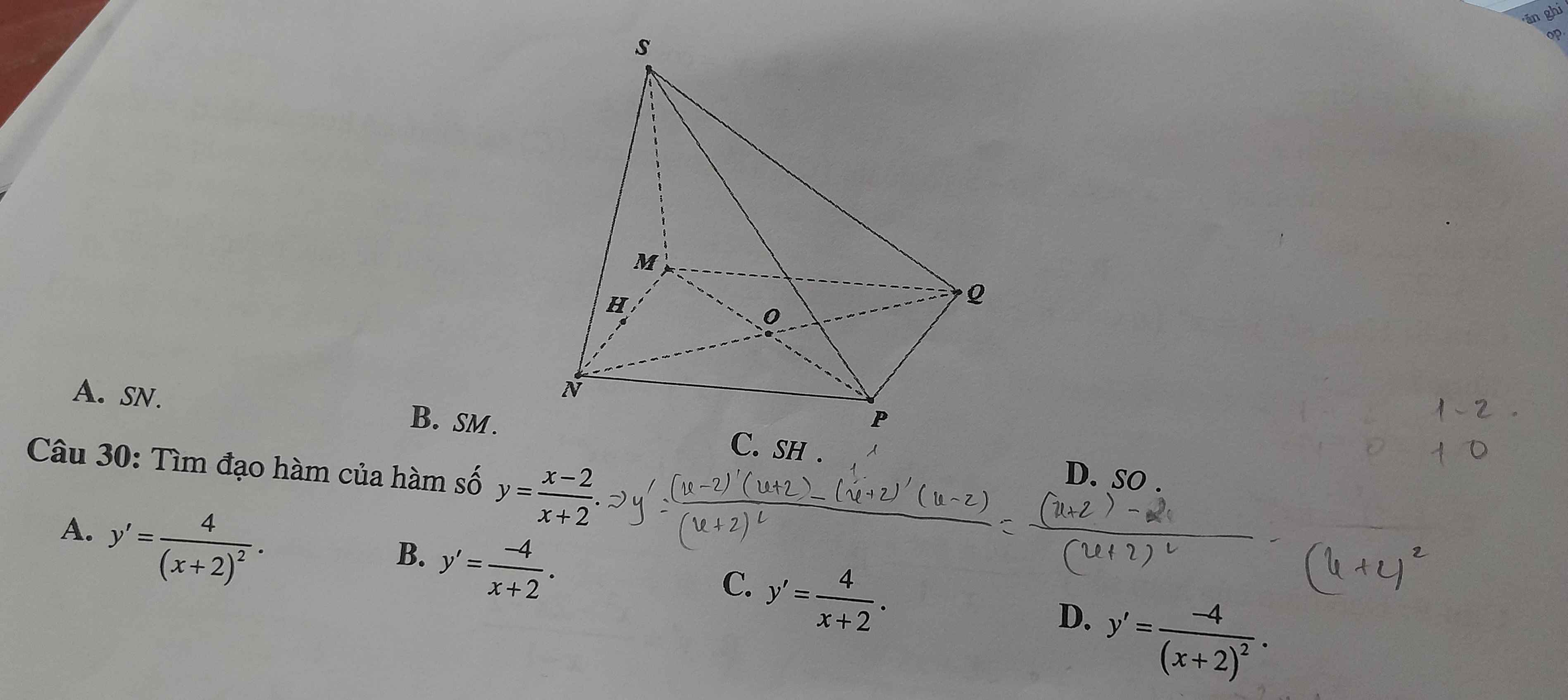
29.

SMN cân tại S \(\Rightarrow SH\perp MN\) (trung tuyến đồng thời là đường cao trong tam giác cân)

Mà \(\left\{{}\begin{matrix}MN=\left(SMN\right)\cap\left(MNPQ\right)\\\left(SMN\right)\perp\left(MNPQ\right)\end{matrix}\right.\)

\(\Rightarrow SH\perp\left(MNPQ\right)\)

Hay SH là đường cao của chóp

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)

\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)

\(f\left(1\right)=m^2-15\)

Hàm liên tục tại \(x=1\) khi:

\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)

\(4^2+\left(-3\right)^2=25\)

\(y'=3x^2-2\)

hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)

\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)

14.

A là khẳng định sai, CD không vuông góc SB

(Vì nếu \(CD\perp SB\)  (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)

(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))

5.

A là mệnh đề sai, vì các mặt bên của chóp đều luôn tạo với đáy các góc bằng nhau

6.

Do tam giác SAB cân tại S \(\Rightarrow SH\perp AB\) (trung tuyến đồng thời là đường cao)

Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\)

\(\Rightarrow SH\perp\left(ABCD\right)\)

Hay SH là đường cao của chóp

24.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

25.

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow\widehat{SAO}\) là góc giữa SA và (ABC)

\(AO=\dfrac{2}{3}.\dfrac{1.\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\)

\(\Rightarrow cos\widehat{SAO}=\dfrac{AO}{SA}=\dfrac{1}{2}\Rightarrow\widehat{SAO}=60^0\)

26.

\(dy=y'dx=\left(x^2\right)'dx=2xdx\)

\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}\dfrac{\sqrt{x^2+7}-4}{2x-6}=\lim\limits_{x\rightarrow3}\dfrac{x^2-9}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)

\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}=\lim\limits_{x\rightarrow3}\dfrac{x+3}{2\left(\sqrt{x^2+7}+4\right)}\)

\(=\dfrac{6}{2\left(4+4\right)}=\dfrac{3}{8}\)

\(f\left(3\right)=1-2m\)

Hàm liên tục trên R khi: 

\(1-2m=\dfrac{3}{8}\Rightarrow m=\dfrac{5}{16}\in\left(0;1\right)\)