mn giúp mink bài 4 tìm Y với, mình cần gấp.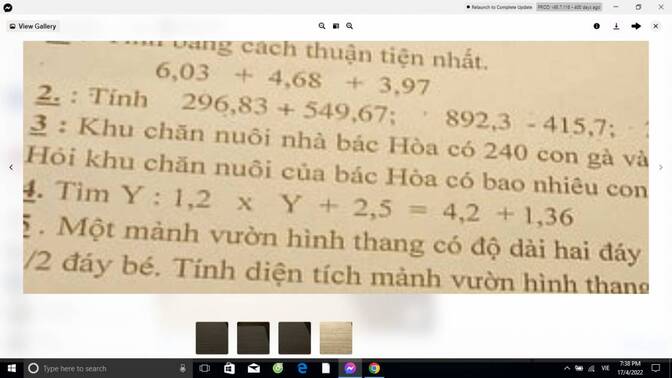

Những câu hỏi liên quan
mn giải giúp mink với mink cần rất gấp
(-4) x y -5=23-32
mn x là nhân nha,mn giúp mink với nhá.Thank you mn thân thương
![]()
 mn giúp mink với. mình cần gấp trong tối nay.
mn giúp mink với. mình cần gấp trong tối nay.
các bn ơi giúp mink bài 4 với mink đang cần gấp lắm ( nếu bn nào lm dc câu e bài 3 thì giúp mink luôn nha mink cảm ơn nhìu lắm :))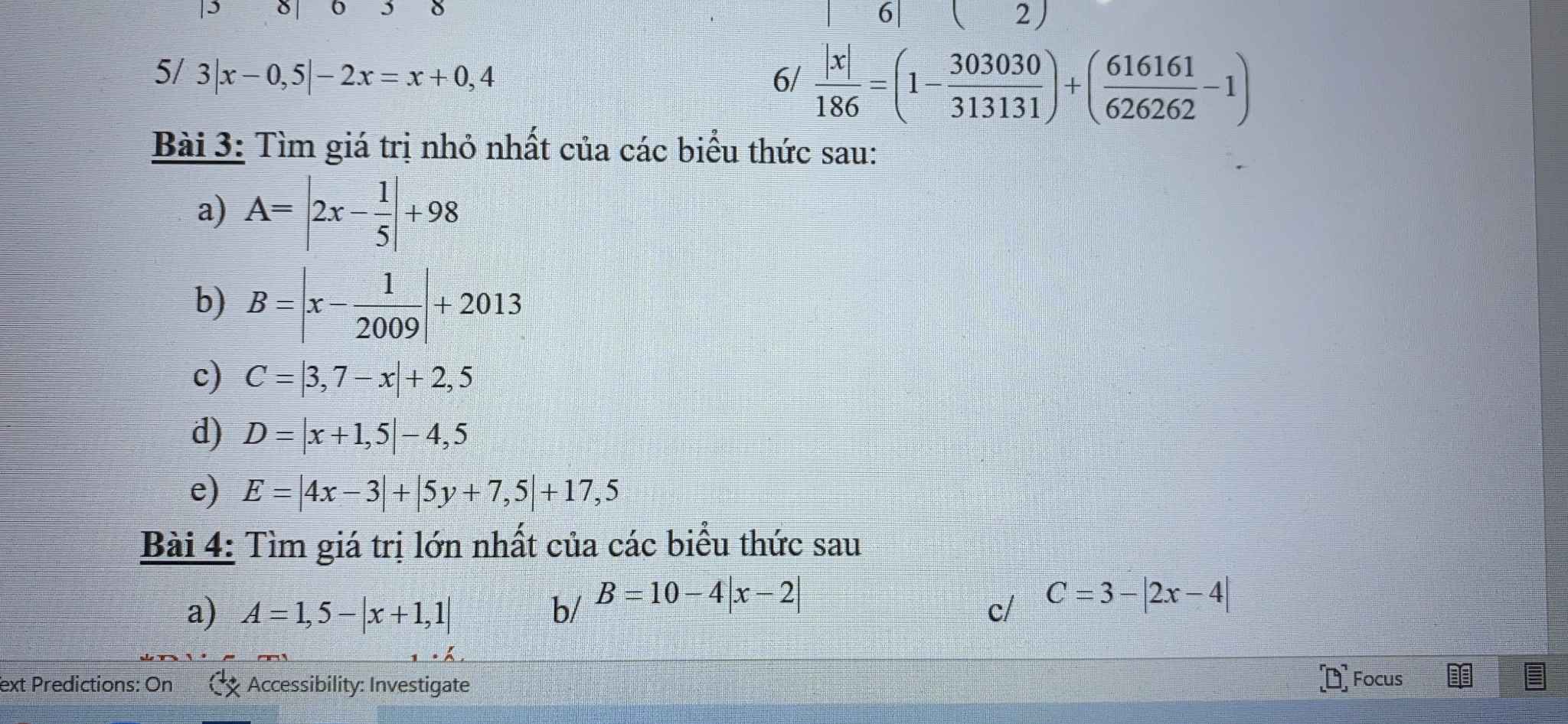
Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 1
Bình luận (1)
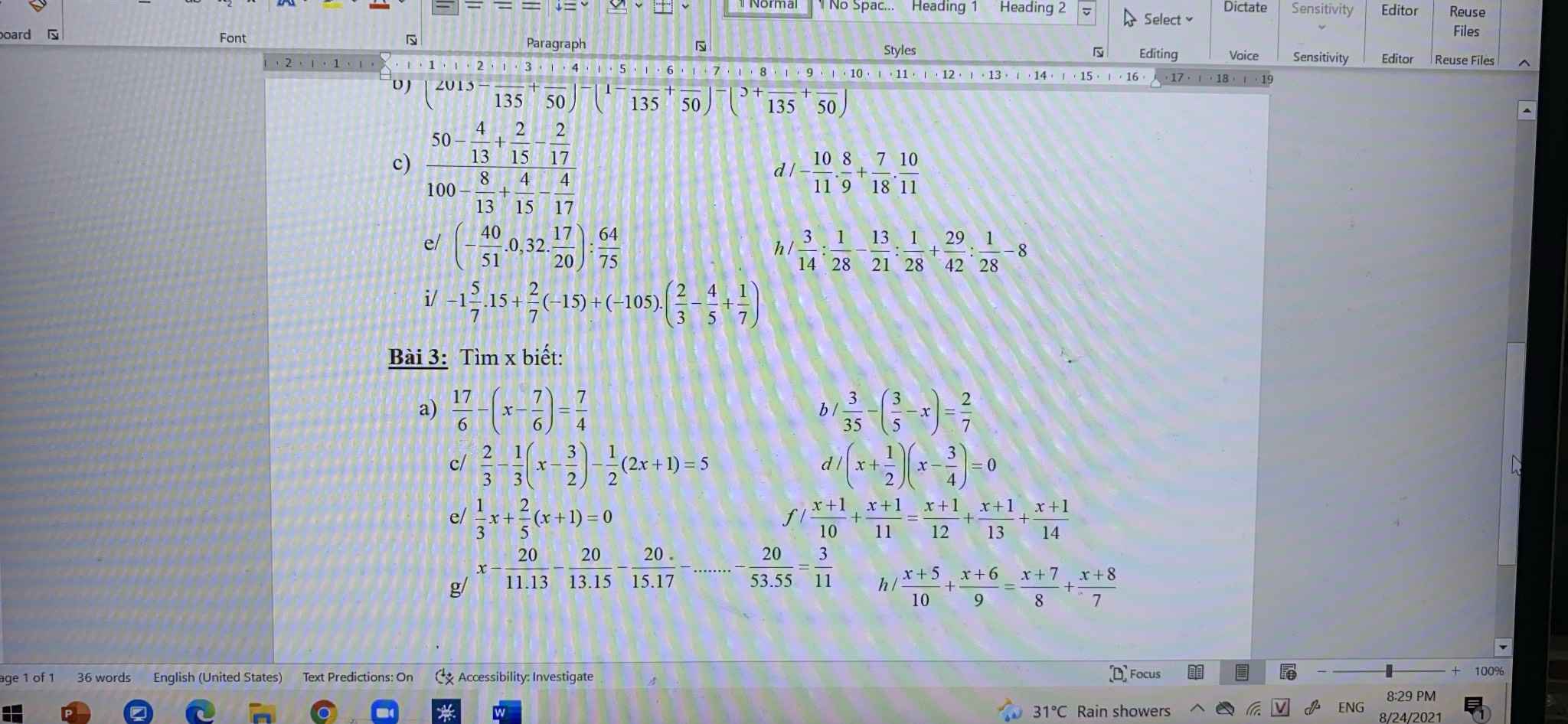
các bạn ơi giúp mink bài 3 với nha mink cần gấp tối nay rồi ! ![]()
giúp mink với nha mink cảm ơn nhìu lắm
Xem thêm câu trả lời
(giải giúp mink bài này với mink đga cần gấp) 
Bài 4: Tìm số tự nhiên nhỏ nhất khi chia cho 3;4;5;10 có số dư lần lượt là 2;3;4;9.
Giúp mink mink cần gấp
Gọi số tự nhiên đó là \(n\).
Số tự nhiên đó khi chia cho \(3,4,5,10\)có số dư lần lượt là \(2,3,4,9\)nên \(n+1\)chia hết cho cả \(3,4,5,10\)
mà \(n\)nhỏ nhất nên \(n+1=BCNN\left(3,4,5,10\right)\).
Phân tích thành tích các thừa số nguyên tố: \(3=3,4=2^2,5=5,10=2.5\)
suy ra \(BCNN\left(3,4,5,10\right)=2^2.3.5=60\)
suy ra \(n+1=60\Leftrightarrow n=59\).
Tìm x, y, z thoả mãn đẳng thức
x+y+z +8=2√(x-1) +4√(y-2) +6√(z-3)
Mn giúp mình với , mình cần gấp lắm
\(x+y+z+8=2\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\) (ĐKXĐ : \(x\ge1;y\ge2;z\ge3\))
\(\Leftrightarrow\left(x-1-2\sqrt{x-1}+1\right)+\left(y-2-4\sqrt{y-2}+4\right)+\left(z-3-6\sqrt{z-3}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2+\left(\sqrt{y-2}-2\right)^2+\left(\sqrt{z-3}-3\right)^2=0\)
Vì \(\left(\sqrt{x-1}-1\right)^2\ge0;\left(\sqrt{y-2}-2\right)^2\ge0;\left(\sqrt{z-3}-3\right)^2\ge0\)
nên phương trình tương đương với : \(\hept{\begin{cases}\left(\sqrt{x-1}-1\right)^2=0\\\left(\sqrt{y-2}-2\right)^2=0\\\left(\sqrt{z-3}-3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\\z=12\end{cases}}}\)(TMĐK)
Vậy nghiệm của phương trình : \(\left(x;y;z\right)=\left(2;6;12\right)\)
Đúng 0
Bình luận (0)
Giúp mình bài 2 với Mn ơi
Mình cần gấp!!! 
Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC
Đúng 0
Bình luận (0)
















