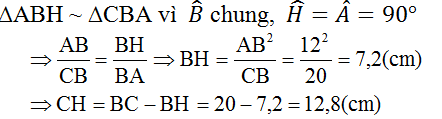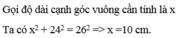tính cạnh góc vuông của 1 tam giác vuông biết cạnh huyền = 13 và cạnh góc vuông kia = 12

Những câu hỏi liên quan
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm
Giả sử ∆ABC có ∠A =90o, BC = 13 cm, AC = 12cm
Theo định lý pitago ta có: BC2 = AB2 + AC2
Suy ra: AB2=BC2-AC2=132-122=25
Vậy AB = 5 cm
Đúng 0
Bình luận (0)
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm
LẤY 13^2- 12^2= 169-144=25 Vậy cạnh góc vuông còn lại sẽ = 5
Đúng 0
Bình luận (0)
Giả sử ∆ABC có \(\widehat{A}\)= \(90^0\), BC = 13 cm, AC = 12cm
Theo định lý Pitago ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
Hay \(AC^2=13^2-12^2\)
\(AC^2=169-144\)
\(AC^2=25\)
\(AC=\sqrt{25}\)
\(AC=5cm\)
Đúng 0
Bình luận (0)
Gọi tam giác đó là ABC có cạnh góc vuông cần tìm là AC, cạnh gócvuông đã biết là AB, cạnh huyền là BC
trong tam giác vuông ABC theo pytago ta có:
\(BC^2=AC^2+AB^2\)
<=> \(13^2=12^2+AC^2\)
<=> \(AC^2=25\) <-> AC = 5
vậy cạnh góc vuông cần tìm là 5cm
~~~~~ chúc bn lul lul hok giỏi ~~~~
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
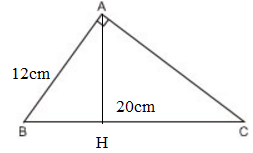
Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12 cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền ?
tính độ dài đường trung tuyến ứng vs cạnh huyền của 1 tam giác vuông, biết rằng tổng độ dài 2 cạnh góc vuông là 47cm và 1 cạnh góc vuông nhỏ hơn cạnh góc vuông kia 23cm.
chứng minh rằng nếu cạnh góc vuông và cạnh huyền của tam giác vuông này tỉ lệ cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó đồng dạng
Xem chi tiết
Gọi 2 tam giác đó lần lượt là `\DeltaABC,\DeltaA'B'C'`
Cạnh góc vuông là cạnh huyền của 2 tam giác lần lượt là `AB,BC` và `A'B',B'C`
Xét tam giác `\DeltaABC` và `\DeltaA'B'C'`:
`(AB)/(BC)=(A'B')/(B'C')`
`\hat{BAC}=\hat{B'A'C'}=90^o`
`=>\DeltaABC~\DeltaA'B'C'`
Đúng 2
Bình luận (0)
Tính độ dài cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 26 cm, cạnh góc vuông kia bằng 24 cm.
Một tam giác vuông có cạnh góc vuông này lớn hơn cạnh góc vuông kia 1m và có cạnh huyền dài 5m .Tính chu vi của tam giác vuông đó?
Gọi x là độ dài cạnh góc vuông nhỏ
Độ dài cạnh góc vuông lớn là: x+1
Theo đề, ta có phương trình:
\(x^2+\left(x+1\right)^2=25\)
\(\Leftrightarrow2x^2+2x+1-25=0\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\left(loại\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
Chu vi tam giác vuông đó là:
\(3+4+5=12\left(m\right)\)
Đúng 1
Bình luận (1)
Gọi cạnh góc vuông nhỏ hơn của tam giác vuông đó là a(m)(a>0)
Theo đề ra, ta có:
\(a^2+\left(a+1\right)^2=25\\ \Rightarrow a^2+a^2+2a+1=25\\ \Rightarrow2a^2+2a=24\\ \Rightarrow a\left(a+1\right)=12=3.4\\ \Rightarrow a=3\)
Chu vi tam giác đó là:
3 + 3 + 1 + 5 = 12(m)
Đúng 1
Bình luận (0)
Tính tỉ số 2 cạnh góc vuông của 1 tam giác vuông biết rằng đường cao và đường trung tuyến ứng với cạnh huyền của tam giác tỉ lệ 12:13
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13cm, cạnh góc vuông kia bằng 12cm ?
Đặt tên cho \(\Delta\) này là \(\Delta\)ABC, ta có:
AB & BC là cạnh góc vuông.
AC là cạnh huyền.
Áp dụng định lý py-ta-go vào \(\Delta\)ABC, ta có:
AC2 = AB2 + BC2
132 = 122 + BC2
169 = 144 + BC2
BC2 = 169 - 144 = 25
BC = \(\sqrt{25}\) = 5cm.
Vậy cạnh BC = 5cm hay cạnh góc vuông còn lại của \(\Delta\) = 5cm.
Đúng 3
Bình luận (0)
Giả sử ∆ABC có ˆA=90∘, BC = 13cm, AC = 12cm
Theo định lý Pytago, ta có: BC2=AB2+AC2
Suy ra: AB2=BC2−AC2=132−122=252
Vậy AB = 5 (cm)
Đúng 1
Bình luận (0)
Đặt tam giác đó là tam giác ABC vuông tại A.
Và BC là cạnh huyền; AB và AC là cạnh góc vuông.
Ta có ABC vuông tại A.
nên BC2=AB2+AC2(định lý Pytago)
Do đó: 132=122+AC2
169=144+AC2
AC2=169-144=25
AC=5(cm)
Vậy cạnh góc vuông cần tìm có độ dài là 5cm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời