Hình Vuông ABCD có cạnh 2 cm . Tính bán kính đường tròn ngoại tiếp , nội tiếp hình vuông ABCD

Những câu hỏi liên quan
bài1.cho hình tròn ngoại tiếp hình vuông abcd có bán kính r bằng 2 cm.tính diện tích hình vuông abcd?bài 2.cho hình tròn nội tiếp hinh vuông abcd biết ac=8 cm.tính diện tích hình tròn?
Cho hình vuông ABCD cạnh a.Gọi O là tâm đường tròn ngoại tiếp hình vuông. Tính bán kính R của (O)? A.
R
a
2
4
B.
R
a
2
C.
R
O
A
a
2
2...
Đọc tiếp
Cho hình vuông ABCD cạnh a.Gọi O là tâm đường tròn ngoại tiếp hình vuông. Tính bán kính R của (O)?
A. R = a 2 4
B. R = a 2
C. R = O A = a 2 2
D. R = a 2
Chọn đáp án C.
Gọi O là tâm của hình vuông ABCD
Khi đó, bán kính đường tròn ngoại tiếp hình vuông ABCD là R = OA
Áp dụng đinh lí Pytago vào tam giác vuông ABC ta có:

Đúng 1
Bình luận (0)
a) Vẽ hình vuông cạnh 4 cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kinh R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
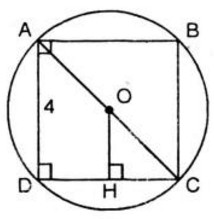
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có tâm O. Gọi R,r là bán kính đường tròn ngoại tiếp và nội tiếp hình vuông ABCD.Kẻ OH⊥CD,chứng minh OH=HD
Cho hình vuông abcd gọi e là trung điểm cạnh ab biết bán kính đường tròn ngoại tiếp Tam giác edc bằng r tính độ dài các cạnh hình vuông abcd theo r
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
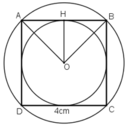
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
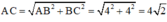 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 4. Gọi M là trung điểm của CD. Tính bán kính đường tròn ngoại tiếp tam giác AMB
Xem chi tiết
HÌNH VUÔNG ABCD NỘI TIẾP (0,2) TÍNH BÁN KÍNH R CỦA đường TRÒN Nội tiếp ABCD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD),
a
3
. Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng
a
3
3
, góc
A
C
B
^
30
∘
. Tính theo a thể tích khối chóp S.ABCD A.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc A C B ^ = 30 ∘ . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. a 3 6
D. 4 a 3 3