12x + 13x = 25

Những câu hỏi liên quan
a)10x+14x+x=100
b) 12x+13x=25
c) 3x+15+30x+25=139
giải hộ mình đc ko ạ ! cảm ơn mng nhiều
a) 10x + 14x + x = 100
x.(10+14+1)=100
x.25=100
x = 4
b) 12x + 13x =25
x.(12+13)=25
x.25=25
x=1
Đúng 0
Bình luận (0)
tim gtnn hoac gtln
a, x^2-8x+21
b,16x^2+16x-30
c,13x^2-39x+15
d,12x+34-x^2
e,-18x-25-6x^2
a: \(x^2-8x+21=x^2-8x+16+5=\left(x-4\right)^2+5>=5\)
Dấu '=' xảy ra khi x=4
b: \(16x^2+16x-30\)
\(=16x^2+2\cdot4x\cdot2+4-34\)
\(=\left(4x+2\right)^2-34>=-34\)
Dấu '=' xảy ra khi x=-1/2
d: \(-x^2+12x+34\)
\(=-\left(x^2-12x-34\right)\)
\(=-\left(x^2-12x+36-70\right)\)
\(=-\left(x-6\right)^2+70< =70\)
Dấu '=' xảy ra khi x=6
Đúng 0
Bình luận (0)
cho x^2=y^2+z^2 chứng minh rằng (13x-12y-5z)(13x-12y+5z)=(12x-13y )^2
Ta có: \(x^2=y^2+z^2\)
\(\Leftrightarrow x^2-y^2=z^2\)
\(\Leftrightarrow25\left(x-y\right)\left(x+y\right)=25z^2\)
\(\Leftrightarrow\left(25x-25y\right)\left(x+y\right)=25z^2\)
\(\Leftrightarrow\left(13x-12y+12x-13y\right)\left(13x-12y-12x+13y\right)=25z^2\)
\(\Leftrightarrow\left(13x-12y\right)^2-\left(12x-13y\right)^2=25z^2\)
\(\Leftrightarrow\left(13x-12y\right)^2-\left(5z\right)^2=\left(12x-13y\right)^2\)
\(\Leftrightarrow\left(13x-12y-5z\right)\left(13x-12y+5z\right)=\left(12x-13y\right)^2\)(ĐPCM).
Đúng 0
Bình luận (0)
bài 1:tìm x
a)25<2 ngũ x<3125 b)(x+1)+(x+2)+(x+3)+....+(x+100)=7450
c)1+2+3+...+x=78 d)12x+13x=2000
e)6x+4x=2010
Ta có:
a)\(25< 2^x< 3125\)
\(\Rightarrow2^4< 2^x< 2^{12}\)
\(\Rightarrow4< x< 12\)
b)\(\left(x+1\right)+\left(x+2\right)+...+\left(x+100\right)=7450\)
\(\Rightarrow100x+5050=7450\Rightarrow10x=2400\Rightarrow x=240\)
c)\(1+2+3+..+x=\frac{x\left(x+1\right)}{2}=78.\)
\(\Rightarrow x\left(x+1\right)=156\)\(\Rightarrow x=12\)
d)\(12x+13x=25x=2000\Rightarrow x=80\)
e)\(6x+4x=10x=2010\Rightarrow x=201\)
12x+12y+13x+13q+14a+14b=100000^2
Giải bất phương trình
log
3
-
1
3
x
-
2
log
3
-
1
2
x
-
1
A. x1 B. x1 C.
1...
Đọc tiếp
Giải bất phương trình log 3 - 1 3 x - 2 > log 3 - 1 2 x - 1
A. x>1
B. x<1
C. 1 2 < x < 1
D. 2 3 < x < 1
Giải phương trình:
1
3
x
−
1
+
1
2
x
+
4
1
9
x
−
2
+
1
5
−
4
x
Đọc tiếp
Giải phương trình: 1 3 x − 1 + 1 2 x + 4 = 1 9 x − 2 + 1 5 − 4 x
1 3 x − 1 + 1 2 x + 4 = 1 9 x − 2 + 1 5 − 4 x Đ K : x ≠ 1 3 , x ≠ − 2 , x ≠ 2 9 , x ≠ 5 4
Ta có pt: 5 x + 3 ( 3 x − 1 ) ( 2 x + 4 ) = 5 x + 3 ( 9 x − 2 ) ( 5 − 4 x )
< = > x = − 3 5 ( 3 x − 1 ) ( 2 x + 4 ) = ( 9 x − 2 ) ( 5 − 4 x ) < = > x = − 3 5 6 x 2 + 12 x − 2 x − 4 = − 36 x 2 + 45 x + 8 x − 10 < = > x = − 3 5 ( T M ) x = 6 7 ( T M ) x = 1 6 ( T M )
Vậy phương trình đã có có 3 nghiệm phân biệt như trên.
Đúng 0
Bình luận (0)
Giải phương trình:
13
x
-
3
2
x
+
7
+
1
2
x...
Đọc tiếp
Giải phương trình: 13 x - 3 2 x + 7 + 1 2 x + 7 = 6 x - 3 x + 3
Điều kiện xác định: x ≠ ±3; x ≠ -7/2.
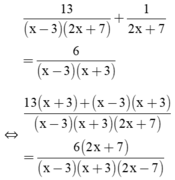
⇒ 13(x + 3) + (x – 3)(x + 3) = 6(2x + 7)
⇔ 13x + 39 + x2 – 9 = 12x + 42
⇔ x2 + x – 12 = 0
⇔ x2 +4x – 3x – 12 = 0
⇔ x(x + 4) – 3(x + 4) = 0
⇔ (x – 3)(x + 4) = 0
⇔ x – 3 = 0 hoặc x + 4 = 0
x – 3 = 0 ⇔ x = 3 (không thỏa mãn đkxđ)
x + 4 = 0 ⇔ x = -4 (thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm S = {-4}.
Đúng 0
Bình luận (0)
C= x^4 - 6^3 + 13x^2 -12x +11















