Cho tam giác ABC cân tại A, đường cao AH=\(a\sqrt{3}\) , BC=3a. BC thuộc (P). Gọi A' là hình chiếu của A lên (P). Tính diện tích tam giác A'BC biết ((P),(ABC))=30

Những câu hỏi liên quan
Cho tam giác cân ABC có đường cao AH asqrt{3}, mặt phẳng đáy BC 3a, BC ⊂(P), A∉(P) . Gọi A là hình chiếu vuông góc của A lên (P). Tam giác ABC vuông tại A. Gọi α là góc giữa (P) và (ABC). Tính α
Đọc tiếp
Cho tam giác cân ABC có đường cao AH = \(a\sqrt{3}\), mặt phẳng đáy BC = 3a, BC ⊂(P), A∉(P) . Gọi A' là hình chiếu vuông góc của A lên (P). Tam giác A'BC vuông tại A'. Gọi α là góc giữa (P) và (ABC). Tính α
Cho tam giác cân ABC có đường cao
A
H
a
3
,
B
C
3
a
,BC chứa trong mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A’BC vuông tại A’. Gọi j là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau? A....
Đọc tiếp
Cho tam giác cân ABC có đường cao A H = a 3 , B C = 3 a ,BC chứa trong mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A’BC vuông tại A’. Gọi j là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau?
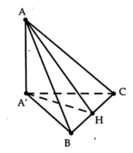
A. φ = 30 o
B. φ = 45 o
C. cos φ = 2 3
D. φ = 60 o
Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
![]()
Do đó:
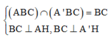
![]()
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
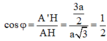
⇒ φ = 60 o
Đúng 0
Bình luận (0)
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 12 cm, AC 16 cm. Vẽ đường cao AH. Vẽ đường phân giác AD của tam giác ABC ( D thuộc BC) a) Tính BC, BD, CD, AH b) Gọi M,N lần lượt là hình chiếu của H lên AB, CD. Tính diện tích tứ giác AMHN. c) Chứng minh AN / AC + AM/AB 1
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 12 cm, AC = 16 cm. Vẽ đường cao AH. Vẽ đường phân giác AD của tam giác ABC ( D thuộc BC)
a) Tính BC, BD, CD, AH
b) Gọi M,N lần lượt là hình chiếu của H lên AB, CD. Tính diện tích tứ giác AMHN.
c) Chứng minh AN / AC + AM/AB = 1
a: \(CB=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=9,6cm
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
b: Sửa đề: AB,AC
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
AM=AH^2/AB=9,6^2/12=7,68(cm)
AN=AH^2/AC=9,6^2/16=5,76(cm)
\(S_{AMHN}=7.68\cdot5.76=44.2368\left(cm^2\right)\)
Đúng 1
Bình luận (0)
1. Cho tam giác ABC vuông tại A, AB=12cm, AC=16cm, vẽ đường cao AH. CM:
a) Tam giác HAC đồng dạng tam giác ABC
b) Gọi AD là tia phân giác của tam giác ABC(D thuộc BC), tính BC,DC?
c) Gọi E là hình chiếu của D lên cạnh AC. CM:AB.CE=DE.AC
d) Tính diện tích tam giác DEC
khi bi phan boi thi lm gi bay gio ha cac b huhu......
Đúng 0
Bình luận (0)
cho tam giác ABC, vuông tại góc A. đường cao AH ( H thuộc BC). biết BH =4cm, CH=9cm. Gọi I,K lần lượt là hình chiếu của tam giác lên cạnh AB, AC. Chứng minh rằng:
a) AIHK là hình chữ nhật.
b) tam giác AKI đồng dạng với tam giác ABC
c) Tính diện tích tam giác ABC
a.Xét tứ giác AIHK có: góc BAC=AIH=AKH=90 ĐỘ
Suy ra AIHK là hình chữ nhật
b.Gọi O là giao điểm của 2 đường chéo hình AIHK
Ta có góc AIO=AHK( tính chất hình chữ nhật )
mà AHK +KHC=90 độ
Góc ACB + KHC cũng bằng 90 độ
nên góc AHK Bằng góc ACB
Nên góc AIK = ACB
Xét tam giác AKI và tam giác ABC có
góc A chung
Góc AIK = ACB (chứng minh trên)
Suy ra Tam giác AKI đồng dạng với tam giác ABC (g.g)
Đúng 1
Bình luận (0)
nguyễn tạ kiều trinh làm sai rồi nhá
Đúng 0
Bình luận (0)
gọi O là giao điểm 2 đường chéo
suy ra IO=IA(tính chất hcn)
suy ra tam giac OAI can tai O
Ta có góc HAB= gocC(cùng phụ góc B)
ta lai co goc A= goc I (t/chat tam gic can)
ma goc A=goc C
nen suy ra gocI= goc C
tg AIK va tg ACB co:
A chung I =C (CMT)
suy ra 2 tam gic dong dang
cau c)
xet tg AHC va tg BhA co
C=BAH(CMT)
AHB=AHC=1v
suy ra 2 tg dong dang
suy ra AH/BH=CH/AH(ti so dong dang)
S ta ABC=1/2AH.BC
AH= ah bình
AH =căn 9.4=6
S tg ABC=1/2.13.6=36
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC vuông tại A , đường cao AH(H thuộc BC) . biết BH bằng 4 cm; CH bằng 9 cm. gọi I, K lần lượt là hình chiếu của H lên AB và AC . chứng minh rằng:
a) tứ giác AIHK là hình chữ nhật
b) tam giác AKI đồng dạng với tam giác ABC
c) tính diện tích tam giác ABC
a) tứ giác AIHK có: góc IAK=AIH=IHK=90 ĐỘ nên là hcn
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A. Biết AB:AC = 2:3, đường cao AH=6cm. Tính các cạnh tam giác ABC.Tam giác ABC cân tại A. Gọi H là hình chiếu của B lên AC. Tính BC, biết AH = 7cm, HC=2cm.Cho a,b,c thuộc đoạn [-1;1] thõa man a+b+c = 0. CMR: \(a^4+b^4+c^4\le2\)
Xem chi tiết
Bài 1 :Cho tam giác ABC vuông tại A , đường cao AH . Gọi E,F lần lượt là hình chiếu của H lên AB,AC. Biết HE 2HF và diện tích AEHF 32 .Tính độ dài các cạnh của tam giác ABC.Bài 2 :Cho hình thang ABCD vuông tại A và D, ADAB2a , CDa . Tính BC và khoảng cách từ trung điểm I của AD đến BC.Bài 3 :Cho tam giác ABC vuông tại A , đường cao AH. Biết AH 24a, BC 50a và AB AC . Tính AB,AC( giúp mình mấy bài này vs , mình cảm ơn )
Đọc tiếp
Bài 1 :
Cho tam giác ABC vuông tại A , đường cao AH . Gọi E,F lần lượt là hình chiếu của H lên AB,AC. Biết HE= 2HF và diện tích AEHF = 32 .Tính độ dài các cạnh của tam giác ABC.
Bài 2 :
Cho hình thang ABCD vuông tại A và D, AD=AB=2a , CD=a . Tính BC và khoảng cách từ trung điểm I của AD đến BC.
Bài 3 :
Cho tam giác ABC vuông tại A , đường cao AH. Biết AH= 24a, BC = 50a và AB <AC . Tính AB,AC
( giúp mình mấy bài này vs , mình cảm ơn )

















