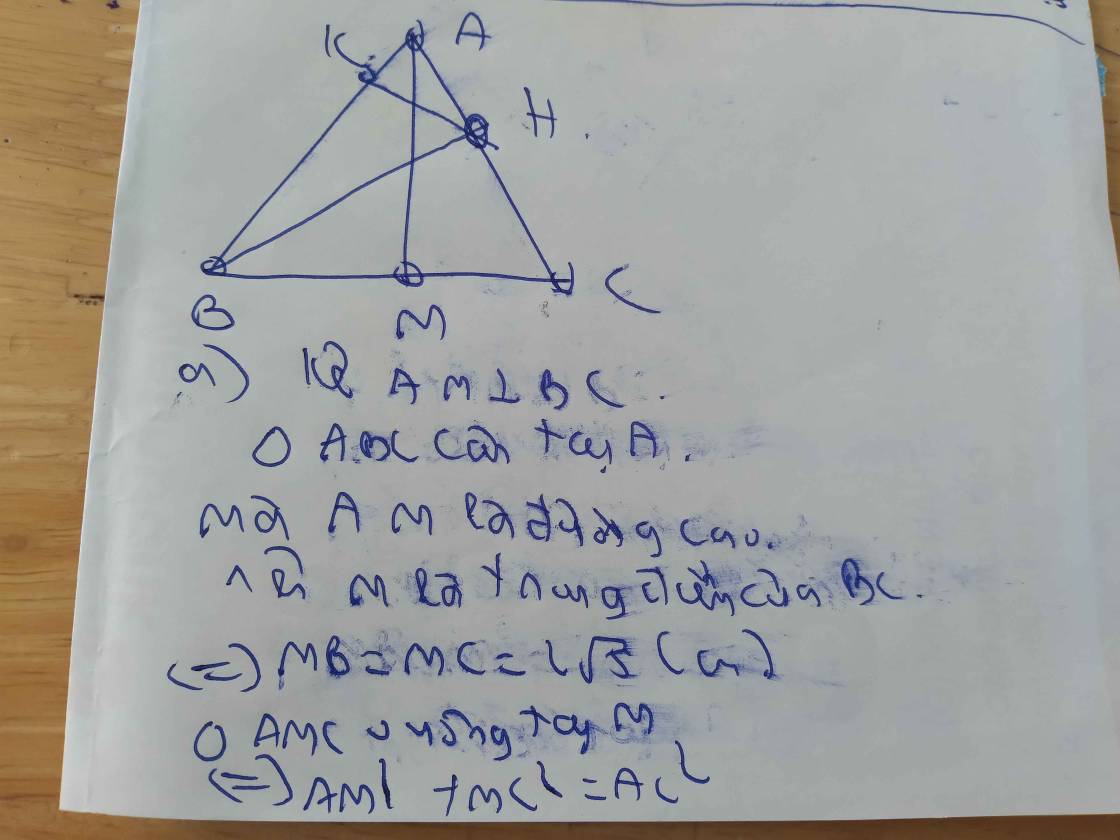
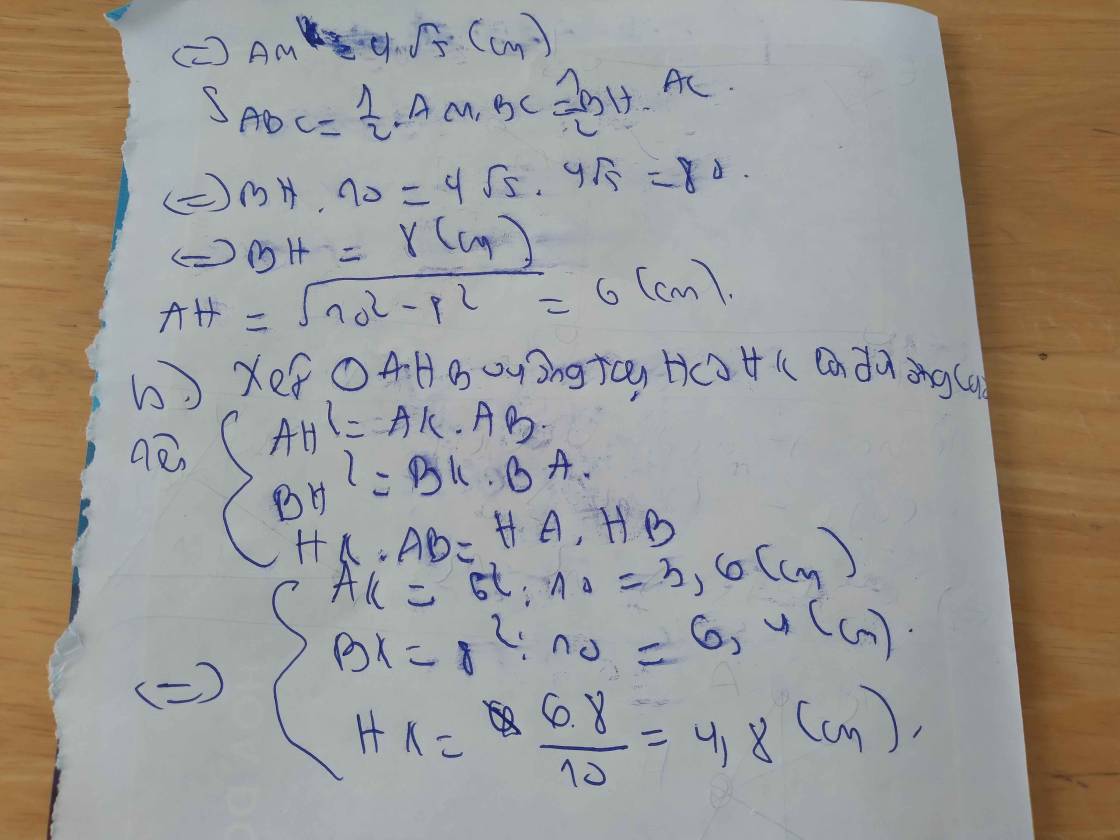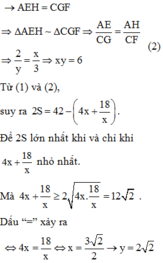1.Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=8cm, HC - HB=8cm
a)Tính HB,HC,AC
b)Vẽ phân giác AD, tính DB, DC, DA.
2. Cho tam giác ABC cân tại A , có AB=AC=10cm, BC= \(4\sqrt{5}\)cm. vẽ đường cao BH.
a) Tính AH
b)Gọi K là hình chiếu của H trên AB. Tính KA, KB, HK
Cho tam giác ABC vuông tại A tính BH,CH, AC ,AH biết:1, AB 12 cm BC 13cm AB 5 cm BC 1dmAB 3sqrt{3} cm BC 9cm2,Tính BC ,AH, BH ,CHAB 24 cm AC 18cmAB 2sqrt{2} cm AC 2sqrt{2}cmAB 3sqrt{3} cm AC 9cm
Đọc tiếp
Cho tam giác ABC vuông tại A tính BH,CH, AC ,AH biết:
1, AB =12 cm BC= 13cm
AB =5 cm BC= 1dm
AB =3\(\sqrt{3}\) cm BC= 9cm
2,Tính BC ,AH, BH ,CH
AB =24 cm AC= 18cm
AB =2\(\sqrt{2}\) cm AC= 2\(\sqrt{2}\)cm
AB =3\(\sqrt{3}\) cm AC= 9cm
Cho tam giác ABC, kẻ đường cao AH. Gọi I và K theo thứ tự là các điểm đối xứng của H qua các cạnh AB và AC. Biết AH = \(2\sqrt{5}\) cm; BH = 4cm; CH = 5cm. (Cho mk xin cách vẽ hình, ko cần làm)
Ta nhận thấy \(AH^2=\left(2\sqrt{5}\right)^2=20\) và \(BH.CH=4.5=20\) và \(AH\perp BC\) tại H nên tam giác ABC sẽ là tam giác vuông tại A. chỉ cần làm như sau:
Vẽ đường thẳng d bất kì. Trên đó lấy 3 điểm B, C, H sao cho H nằm giữa B và C thỏa mãn \(BH=4cm,CH=5cm\)

Sau đó, ta chỉ cần dựng đường thẳng qua H vuông góc với BC cắt đường tròn đường kính BC tại A là xong.

Sau đó ta xóa đi các chi tiết thừa và được hình vẽ đúng theo ycbt.

Đúng 2
Bình luận (0)
Lê Song Phương, em ơi, em vẽ hình đẹp quá, thế điểm I; K đối xứng với H qua AB và AC của cô đâu rồi nhỉ?
Bài này chỉ cần vẽ hình,nhưng cô tìm mãi vẫn chưa thấy I và K đâu em ha!
Đúng 0
Bình luận (0)
Dạ thưa cô, em nghĩ là cái đó bạn tự dựng được nên em chỉ cái khó nhất cho bạn ấy thôi ạ.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A , có AB=AC=10cm, BC= 4√5 4 5 cm. vẽ đường cao BH. a) Tính AH b)Gọi K là hình chiếu của H trên AB. Tính KA, KB, HK.
* Cho tam giác ABC, biết rằng AB=9cm, AC=12cm, BC=15cm, AH là đường cao
a. CM: ΔABC vuông
b. Tính AH, BH
c. Vẽ HE vuông góc AB tại E, Vẽ HI vuông góc AC tại I. CM: AE.AB=AI.AC
d. CM: \(\sqrt{BH.HC}\le\dfrac{BC}{2}\)
Kdfrac{2sqrt{x}-9}{x-5sqrt{x}+6}-dfrac{sqrt{x}+3}{sqrt{x}-2}-dfrac{2sqrt{x}+1}{3-sqrt{x}}
a. Rút gọn K
b.Tìm x để K1
Bài 2 : cho tam giác ABC vuông tại A có đường cao AH . Vẽ HD vuông góc với AB tại D , HE vuông góc với AC tại E
a,Biết AB 8 , AC 10. Tính AH, HB ,HC
b, CM ^{dfrac{AD}{BD}dfrac{AH^2}{BH^2}}
c , CM AH^3 BD . CE. BC
Đọc tiếp
\(K=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
a. Rút gọn K
b.Tìm x để K<1
Bài 2 : cho tam giác ABC vuông tại A có đường cao AH . Vẽ HD vuông góc với AB tại D , HE vuông góc với AC tại E
a,Biết AB =8 , AC= 10. Tính AH, HB ,HC
b, CM \(^{\dfrac{AD}{BD}=\dfrac{AH^2}{BH^2}}\)
c , CM \(AH^3\) = BD . CE. BC
Bài 2:
a: \(BC=\sqrt{10^2+8^2}=2\sqrt{41}\left(cm\right)\)
\(AH=\dfrac{8\cdot10}{2\sqrt{41}}=\dfrac{40}{\sqrt{41}}\left(cm\right)\)
\(BH=\dfrac{64}{2\sqrt{41}}=\dfrac{32}{\sqrt{41}}\left(cm\right)\)
\(CH=\dfrac{100}{2\sqrt{41}}=\dfrac{50}{\sqrt{41}}\left(cm\right)\)
b: \(\dfrac{AD}{BD}=\dfrac{AH^2}{AB}:\dfrac{BH^2}{AB}=\dfrac{AH^2}{BH^2}\)
Đúng 0
Bình luận (0)
Bài 1: Cho bt Pleft(frac{1}{x+sqrt{x}}-frac{1}{sqrt{x}+1}right):frac{sqrt{x}-1}{x+2sqrt{x}+1}a, Rút gọnb, Tìm tất cả các giá trị của x để P-frac{3}{2}Bài 2: Cho △ABC nhọn, đường cao AH. Gọi D,E là hình chiếu của H trên AB,AC. cm:a, AD.AB AE.ACb, AHfrac{BC}{cot B+cot C}c, frac{1}{DH^2}+frac{1}{EH^2}frac{2}{AH^2}+frac{1}{BH^2}+frac{1}{CH^2}d, cotA + cotB + cotC frac{AB^2+AC^2+BC^2}{4S} (S là diện tích △ABC)
Đọc tiếp
Bài 1: Cho bt P=\(\left(\frac{1}{x+\sqrt{x}}-\frac{1}{\sqrt{x}+1}\right):\frac{\sqrt{x}-1}{x+2\sqrt{x}+1}\)
a, Rút gọn
b, Tìm tất cả các giá trị của x để P=\(-\frac{3}{2}\)
Bài 2: Cho △ABC nhọn, đường cao AH. Gọi D,E là hình chiếu của H trên AB,AC. cm:
a, AD.AB = AE.AC
b, AH=\(\frac{BC}{\cot B+\cot C}\)
c, \(\frac{1}{DH^2}+\frac{1}{EH^2}=\frac{2}{AH^2}+\frac{1}{BH^2}+\frac{1}{CH^2}\)
d, cotA + cotB + cotC =\(\frac{AB^2+AC^2+BC^2}{4S}\) (S là diện tích △ABC)
Con gái hay con trai mà chăm dữ cha :o 12h đêm lun
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Đường cao AH. Gọi M,N là hình chiếu của H trên AC,AB.
Chứng minh rằng:
a, \(\sqrt[3]{BC^2}\)=\(\sqrt[3]{BN^2}\)+\(\sqrt[3]{CM^2}\)
b, BN\(\sqrt{CH}\)+CM\(\sqrt{BH}\)=AH\(\sqrt{BC}\).
câu a) bn có thể vào câu hỏi tương tự xem, cái này làm vui thôi
Ta có: \(BN=\frac{BH^2}{AB};CM=\frac{CH^2}{AC};AB.AC=AH.BC;BH.CH=AH^2\)
\(\sqrt[3]{BC^2}=\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\)
\(\Leftrightarrow\)\(BC^2=BN^2+CM^2+3\sqrt[3]{\left(BN.CM\right)^2}\left(\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\right)\)
\(\Leftrightarrow\)\(BC^2=BH^2-NH^2+CH^2-MH^2+3\sqrt[3]{\left(\frac{\left(BH.CH\right)^2}{AB.AB}\right)^2}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=\left(BH^2+CH^2\right)-\left(NH^2+MH^2\right)+3\sqrt[3]{\left(\frac{AH^4}{AH.BC}\right)^2}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=\left(BH+CH\right)^2-2BH.CH-\left(NH^2+MH^2\right)+3\sqrt[3]{\frac{AH^6}{BC^2}}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=BC^2-2AH^2-AH^2+3AH^2\) ( do \(NH^2=AM^2\) )
\(\Leftrightarrow\)\(BC^2=BC^2\) ( luôn đúng )
\(\Rightarrow\)\(\sqrt[3]{BC^2}=\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\) đúng
Đúng 0
Bình luận (0)
b) bằng một cách nào đó \(\Delta NBH\) đã đồng dạng với \(\Delta ABC\) ( có góc B chung ) \(\Rightarrow\)\(\frac{BN}{AB}=\frac{BH}{BC}\)
Tương tự: \(\Delta MHC~\Delta ABC\) ( có góc C chung ) \(\Rightarrow\)\(\frac{CM}{AC}=\frac{CH}{BC}\)
\(\Rightarrow\)\(\frac{BN}{AB}+\frac{CM}{AC}=\frac{BH+CH}{BC}=1\)
\(\Leftrightarrow\)\(BN.AC+CM.AB=AB.AB\)
\(\Leftrightarrow\)\(BN\sqrt{AC^2}+CM\sqrt{AB^2}=AB.AC\)
\(\Leftrightarrow\)\(BN\sqrt{CH.BC}+CM\sqrt{BH.BC}=AH.BC\)
\(\Leftrightarrow\)\(BN\sqrt{CH}+CM\sqrt{BH}=AH\sqrt{BC}\) ( chia 2 vế cho \(\sqrt{BC}\ne0\) ) đpcm
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD ( AB//CD) , AB=5 cm , CD=13 cm , BD vuông góc BC . Vẽ đg cao AH
a, Tính độ dài HC
b, Tính BH và diện tích hình thang
Cho một tấm nhôm hình vuông cạnh 6cm. Người ta muốn cắt một hình thang như hình vẽ. Trong đó
A
E
2
(
c
m
)
,
A
H
x
(
c
m
)
,
C
F...
Đọc tiếp
Cho một tấm nhôm hình vuông cạnh 6cm. Người ta muốn cắt một hình thang như hình vẽ. Trong đó A E = 2 ( c m ) , A H = x ( c m ) , C F = 3 ( c m ) , C G = y ( c m ) . Tìm tổng x+y để diện tích hình thang đạt giá trị nhỏ nhất
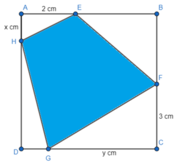
A.x+y=7
B.x+y=5
C. x + y = 7 2 2
D. x + y = 4 2