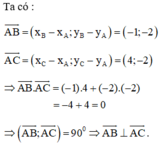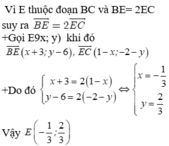Trên mặt phẳng tọa độ Oxy, cho ba điểm A(– 2; 4), B(– 3; 1), C(1; 5). Diện tích tam giác ABC bằng?

Những câu hỏi liên quan
Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Chứng minh AB→ ⊥ AC→.
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C. A.
N
2
;
-
4
7
;
0
B. N(2;0;0) C.
N
2
;
7
4...
Đọc tiếp
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
A. N 2 ; - 4 7 ; 0
B. N(2;0;0)
C. N 2 ; 7 4 ; 0
D. N(0;0;2)
Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6,3) ; B(-3;6) và C(1; -2). Xác định điểm E trên cạnh BC sao cho BE 2EC. A.
E
-
1
3
;
2
3
B.
E
-
1
3
;
-...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6,3) ; B(-3;6) và C(1; -2). Xác định điểm E trên cạnh BC sao cho BE= 2EC.
A. E - 1 3 ; 2 3
B. E - 1 3 ; - 2 3
C. E 2 3 ; - 1 3
D. E - 2 3 ; 1 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho
M
A
→
+
M
B
→
+
M
C
→
có g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất
A. M(-2;-1;0)
B. M(-2;-1;0)
C. M(2;-1;0)
D. M(2;1;0)
Trên mặt phẳng tọa độ Oxy cho điểm A(1;1) và B (-2;-5) ,biết C là một điểm thuộc trục tung sao cho ba điểm A,B,C thẳng hàng . Tung độ của điểm C là gì ?
Câu 2. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1):y=x+2 (d2):y=-x+4 và (d_{3}):y=mx+m. (m là tham số thục). a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ Oxy. b) Xác định các giá trị của tham số m để đường thẳng (d3) đi qua giao điểm của (d1)và(d2)
a: 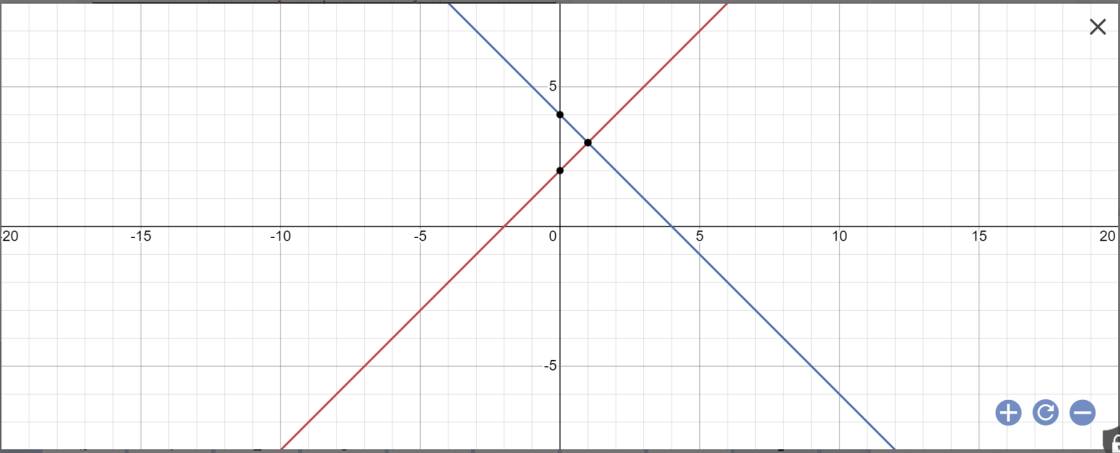
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho ba điểm A(1;4),B(-3;-4),C(1;0). Tính diện tích tam giác ABC.
Ta có :
AB = \(\sqrt{\left(1+3\right)^2+\left(4+4\right)^2}=4\sqrt{5}\)
AC = \(\sqrt{\left(1-1\right)^2+\left(4-0\right)^2}=4\)
BC = \(\sqrt{\left(-3-1\right)^2+\left(-4-0\right)^2}=4\sqrt{2}\)
=> p = \(\frac{4\sqrt{5}+4+4\sqrt{2}}{2}\)
=> \(S_{\Delta ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}=\sqrt{64}=8\)
( TÍNH THEO CÔNG THỨC HERON )
Đúng 0
Bình luận (0)
Ta có :
AB = √(1+3)2+(4+4)2=4√5
AC = √(1−1)2+(4−0)2=4
BC = √(−3−1)2+(−4−0)2=4√2
=> p = 4√5+4+4√22
=> SΔABC=√p(p−AB)(p−AC)(p−BC)=√64=8
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho ba điểm A, B, C có tọa độ như sau: A(7;7), B(2;5), C(5;2). Hãy viết phương trình của các đường thẳng AB, BC và CA.
* Gọi phương trình đường thẳng AB là y = ax + b.
Tọa độ các điểm A, B phải thỏa mãn phương trình y = ax + b nên ta có:
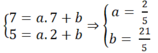
Vậy phương trình của đường thẳng AB là y = 2/5x + 21/5.
*Gọi phương trình của đường thẳng BC là y = a’x + b’.
Tương tự như trên ta có:
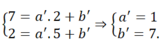
Vậy phương trình của đường thẳng BC là y = -x + 7.
*Gọi phương trình của đường thẳng AC là y = a’’x + b’’.
Tương tự như trên ta có: 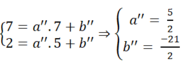
Vậy phương trình của đường thẳng AC là y = 5/2x - 21/2.
Đúng 1
Bình luận (1)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4); B(1;-3;1); C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy) A.
l
2
13
B.
l
2
41
C.
l
2
26
D.
l
2
11
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4); B(1;-3;1); C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy)
A. l = 2 13
B. l = 2 41
C. l = 2 26
D. l = 2 11
Đáp án C
Gọi I(x;y;0) là tâm của mặt cầu (S) ⇒ A I → = x - 1 ; y - 2 ; 4 A I → = x - 1 ; y + 3 ; - 1 A I → = x - 2 ; y - 2 ; - 3
Theo bài ra, ta có
I A = I B I A = I C ⇒ x - 1 2 + y - 2 2 + 4 2 = x - 1 2 + y + 3 2 + - 1 2 x - 1 2 + y - 2 2 + 4 2 = x - 2 2 + y - 2 2 + - 3 2 ⇔ x = - 2 y = 1
Vậy I ( - 2 ; 1 ; 0 ) ⇒ A I → = ( - 3 ; - 1 ; 4 ) ⇒ l = 2 . I A = 2 16 .
Đúng 0
Bình luận (0)