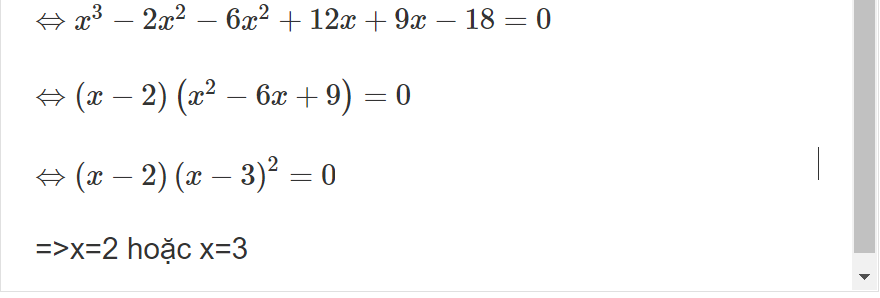8x-2<4x+18

8x-4x<2+18

4x<20

x<5

8x-2<4x+18

=>8x<4x+18+2

=>8x<4x+20

=>2x<20

=>x<20

vậy....

\(\Leftrightarrow x^3-2x^2-6x^2+12x+9x-18=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-6x+9\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)

=>x=2 hoặc x=3

\(A=\dfrac{4\left(x^2+2x+3-3\right)+18}{x^2+2x+3}=\dfrac{4\left(x^2+2x+3\right)+6}{x^2+2x+3}=4+\dfrac{6}{\left(x+1\right)^2+2}\)

Ta có \(\left(x+1\right)^2+2\ge2\Rightarrow\dfrac{6}{\left(x+1\right)^2+2}\le3\Leftrightarrow4+\dfrac{6}{\left(x+1\right)^2+2}\le7\)

Dấu ''='' xảy ra khi x = -1 

=\(\dfrac{18}{7}\)

\(...P=x^2-8x+16+x^2+2xy+y^2+2y^2-2y+2\)

\(P=\left(x-4\right)^2+\left(x+y\right)^2+2\left(y^2-y+1\right)\left(1\right)\)

Xét \(y^2-y+1=y^2-y+\dfrac{1}{4}-\dfrac{1}{4}+1=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\left(\left(y-\dfrac{1}{2}\right)^2\ge0\right)\)

\(\Rightarrow2\left(y^2-y+1\right)\ge2.\dfrac{3}{4}=\dfrac{3}{2}\)

mà \(\left(x-4\right)^2\ge0;\left(x+y\right)^2\ge0\)

\(\left(1\right)\Rightarrow P\ge\dfrac{3}{2}\Rightarrow Min\left(P\right)=\dfrac{3}{2}\)

SORRY LỘN