Cho tam giác ABC có AB = 6 cm; AC = 8 cm, BC= 10cm. a. Tam giác ABC là tam giác gì? Vì sao? b. Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy E sao cho DE = DA. Chứng minh CE song song với AB. giúp mình với ạ

Những câu hỏi liên quan
Cho tam giác ABC có AB = 6 cm ; AC = 8 cm ; BC = 10 cm . CM : Tam giác ABC là tam giác vuông .
Áp dụng định lý Py-ta-go đảo vào tam giác ABC, có:
AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Suy ra tam giác ABC vuông
!
Đúng 0
Bình luận (0)
+ Xét tam giác ABC có :
AB^2+AC^2=100
BC^2=10^2=100
=> AB^2+ AC^2= 100=BC^2
=> tam giác ABC vuông tại A ( Py-ta-go)
Đúng 0
Bình luận (0)
+ Xét tam giác ABC có :
AB^2+AC^2=100
BC^2=10^2=100
=> AB^2+ AC^2= 100=BC^2
=> tam giác ABC vuông tại A ( Py-ta-go)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có AB =6 cm, AC =8 cm, BC =10 cm. Chứng tỏ tam giác ABC vuông.
Ta thấy BC là cạnh lớn nhất
Ta có: \(AB^2+AC^2=6^2+8^2=100.\)
\(BC^2=10^2=100\)
\(\Rightarrow BC^2=AB^2+AC^2\)
Xét tam giác ABC có \(BC^2=AB^2+AC^2\)
=> TAM GIÁC ABC vuông tại A( Py-ta-go đảo)
Cho tam giác ABC có AB = 6 cm AC = 9 cm một đường thẳng d cắt AB ,AC tại E và F sao cho ae = af = 4 cm biết tam giác ABC có diện tích là 27 cm vuông Hỏi diện tích tam giác aef bằng bao nhiêu.các bạn ơi giúp mình với
Xem chi tiết
Hai tam giác AEF và ABF có chung đường cao hạ từ F nên ta có \(\frac{S_{AEF}}{S_{ABF}}=\frac{AE}{AB}=\frac{4}{6}=\frac{2}{3}\)(1)
Hai tam giác ABF và ABC có chung đường cao hạ từ B nên ta có \(\frac{S_{ABF}}{S_{ABC}}=\frac{AF}{AC}=\frac{4}{9}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{S_{AEF}}{S_{ABF}}.\frac{S_{ABF}}{S_{ABC}}=\frac{2}{3}.\frac{4}{9}\)\(\Rightarrow\frac{S_{AEF}}{S_{ABC}}=\frac{8}{27}\)\(\Rightarrow S_{AEF}=\frac{8}{27}S_{ABC}=\frac{8}{27}.27=8\left(cm^2\right)\)
Vậy \(S_{AEF}=8cm^2\)
Bạn vào thống kê hỏi đáp của mình xem câu trả lời nhé. Nó chưa duyệt lên.
cho tam giác ABC vuông tại A có AB = 6 cm BC = 10 cm vẽ đường cao AH của tam giác ABC( H thuộc BC )
1 cm tam giác ABC đồng dạng tam giác hba
2 cm AB bình = BC.BH áp dụng tính HB
3 tia phân giác của góc B cắt AC tại K cmr AK.AC=AH.KC
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có \(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3.6\left(cm\right)\)
3: Xét ΔBAC có BK là đường phân giác
nên \(\dfrac{AK}{KC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
nên \(\dfrac{AK}{KC}=\dfrac{BH}{AB}\left(1\right)\)
Xét ΔAHC vuông tại H và ΔBHA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó: ΔAHC\(\sim\)ΔBHA
Suy ra: \(\dfrac{AC}{AB}=\dfrac{AH}{BH}\)
=>BH/AH=AB/AC
hay \(\dfrac{BH}{AB}=\dfrac{AH}{AC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AK}{KC}=\dfrac{AH}{AC}\)
hay \(AK\cdot AC=AH\cdot KC\)
Đúng 4
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH, AB=6 cm ,AC=8cm
a)CM tam giác ABH đồng dạng vs Tam giác ABC . CM tam giác AHC đồng dạng vs Tam giác ABC
b)CM tam giác AHB đồg dạng vs tam giác AHC
c) Tính BH
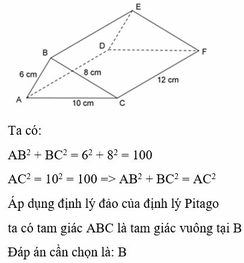
Cho hình lăng trụ đứng ABC.DEF, đáy là tam giác ABC có AB = 6 cm, BC = 8 cm, AC = 10 cm và chiều cao của lăng trụ là 12 cm. Tam giác ABC là tam giác gì?
A. Vuông tại A
B. Vuông tại B
C. Vuông tại C
D. Đều
cho tam giác ABC có AB=6 cm, AC=9 cm. các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho BD=4 cm, CE=6 cm.
1)chứng minh rằng tam giác ADE đồng dạng tam giác ABC, tính tỉ số đồng dạng.
2)kẻ EK//AB(K thuộc BC) chứng minh rằng tam giác ade đồng dạng tam giác ekc
3) tính chu vi tam giác EKC biết BC = 12 cm
Giải chi tiết Cho tam giác ABC có AB 6 cm; AC 8 cm; BC 10 cm.a) Chứng minh tam giác ABC vuông tại A.b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE ^ BC (E Î BC). Chứng minh DA DE. c) Kéo dài ED và BA cắt nhau tại F. Chứng minh tam giác BFC când) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC.
Đọc tiếp
Giải chi tiết Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm.
a) Chứng minh tam giác ABC vuông tại A.
b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE ^ BC (E Î BC).
Chứng minh DA = DE.
c) Kéo dài ED và BA cắt nhau tại F. Chứng minh tam giác BFC cân
d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC.
a. Ta có: \(AB^2+AC^2=6^2+8^2=100=BC^2\)
Áp dụng định lí Py-ta-go đảo ta có: tam giác ABC vuông tại A
b. Xét \(\Delta ABD\) vuông tại A và \(\Delta EBD\) vuông tại E có: \(\left\{{}\begin{matrix}BDchung\\\widehat{ABD}=\widehat{EBD}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ABD\)=\(\Delta EBD\) \(\Rightarrow\)DA=DE(dpcm)
c. Xét \(\Delta FAD\) vuông tại A và \(\Delta CED\) vuông tại E có: \(\left\{{}\begin{matrix}DA=DE\\\widehat{ADF}=\widehat{EDC}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta FAD\)=\(\Delta CED\)\(\Rightarrow\)AF=EC
Mà BF=AB+BF, BC=BE+EC, AF=EC, AB=BE
\(\Rightarrow\)BF=BC\(\Rightarrow\)\(\Delta BFC\) cân tại B
d. Xét \(\Delta BFC\) cân tại B có: CA,FE là đường cao giao nhau tại D
\(\Rightarrow\)BD cũng là đường cao của \(\Delta BFC\)
mà \(\Delta BFC\) cân tại B nên BD vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\) BD là đường trung trực (dpcm)
Đúng 2
Bình luận (1)
B1:Cho tam giác Abc có BC=7,5 cm;CA=4,5 cm;AB=6 cm.Tam giacs Abc là tam giác j?Tính đường cao AH của tam giác abc,biết HB=4,8 cm
B2:Cho hình vuông ABCD có độ dài cạnh bằng 4 cm,1 đường thẳng đi qua C cắt cạnh AD tại K.Biết CK=5 cm.Tính chiều cao BH của tam giác BKC
B4:Cho tam giác Abc đều có cạnh là 6 cm
a)Kẻ đường cao AH.Tính AH?
b)Tính diện tích tam giác Abc?
Cho tam giác ABC có AB=6 cm ; AC = 4,5 cm : BC= 7,5 cm
a) Chứng minh tam giác ABC vuông ở A
Tính góc B ; góc C ; đường cao AH của tam giác ABC
b) Tìm tập hợp điểm M sao cho S tam giác ABC = S tam giác BMC