Tham khảo:

+) Biểu diễn: \(A \subset B\)

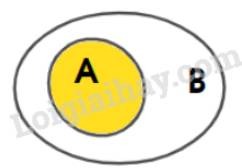
+) Sau đó, biểu diễn: \(B \subset C\)

Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)

Số phần tử của a chắc chắn nhỏ hơn b

VD:a={4;5;3}

      b={9;4;5;3;7}

Bạn đang có nhầm lẫn gì đó về tập hợp . Trong tập hợp không có từ '' con thực sự ''

 Nếu A là con của B nghĩa là tất cả các phần tử của A đều có trong B mà B còn phải có thêm ít nhất một phần tử nữa nên chắc chắn số phần tử của A nhỏ hơn số phần tử của B . 

VD : A = { 1 ; 2 ; 3 ; 4 ; 5 ; .... }

B = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; ..... }

=> \(A\subset B\)

thế mấy phần khác thì sao

giup mk đi mấy bạn

a.ko thế khẳng định số phần tử của a nhỏ hơn số phần tử của b.vì TH a có thể là những phần tử bất kì.ko có VDMH ^_^

b.  nếu a là con thực sự của b thì số phần tử của a ko nhỏ hơn số phần tử của b.vì sao thì đi hỏi thầy

c. Botay.com.vn

a,b,c đúng

d,e sai

c) 2 phan tu tich nha

c, gồm có 2 phần tử đó là 0 và 2

c bạn nha

a) khẳng định a đúng

b) khẳng định b sai

a) Khẳng định sai.

b) Khẳng định đúng.

a) Khẳng định sai.

b) Khẳng định đúng.

Ta có : 

Tập hợp A các stn nhỏ hơn 40 là bội của 6 là :

A = {0;6;12;18;24;30;36}

Tập hợp B các stn nhỏ hơn 40 là bội của 9 là :

B = {0;9;18;27;36}

a)M = {0;18;36}

b)McA       McA

Câu 1: D

Câu 2: B

Câu 3: B

Câu 4: B

Câu 6: D

Không thể .

tick cho mk nha!

a: A={x\(\in R\)|x^2+x-6=0 hoặc 3x^2-10x+8=0}

=>x^2+x-6=0 hoặc 3x^2-10x+8=0

=>(x+3)(x-2)=0 hoặc (x-2)(3x-4)=0

=>\(x\in\left\{-3;2;\dfrac{4}{3}\right\}\)

=>A={-3;2;4/3}

B={x\(\in\)R|x^2-2x-2=0 hoặc 2x^2-7x+6=0}

=>x^2-2x-2=0 hoặc 2x^2-7x+6=0

=>\(x\in\left\{1+\sqrt{3};1-\sqrt{3};2;\dfrac{3}{2}\right\}\)

=>\(B=\left\{1+\sqrt{3};1-\sqrt{3};2;\dfrac{3}{2}\right\}\)

A={-3;2;4/3}

b: \(B\subset X;X\subset A\)

=>\(B\subset A\)(vô lý)

Vậy: KHông có tập hợp X thỏa mãn đề bài