Cho tam giác ABC vuông tại C có AB= 25 cm, AC= 15 cm. Tính độ dài cạnh BC

Những câu hỏi liên quan
Cho tam giác \(ABC\) vuông tại \(A\).
a) Tính độ dài cạnh \(BC\) nếu biết \(AB = 7\)cm, \(AC = 24\)cm.
b) Tính độ dài cạnh \(AB\) biết \(AC = 2\)cm, \(BC = \sqrt {13} \)cm.
c) Tính độ dài cạnh \(AC\) nếu biết \(BC = 25\)cm, \(AB = 15\)cm.
a: BC=căn 7^2+24^2=25cm
b: AB=căn BC^2-AC^2=3(cm)
c: AC=căn 25^2-15^2=20cm
Đúng 0
Bình luận (0)
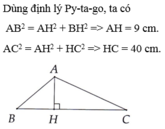
cho tam giác ABC có góc BAC>90 độ . Kẻ AH vuông góc BC tại H. Biết AB=15 cm, AC=41 cm, BH=12 cm . Tính độ dài cạnh HC
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
Đúng 1
Bình luận (0)
Bài 15: Cho tam giác ABC vuông tại A, có AC = 20 cm; AB = 15 cm. Gọi M là trung điểm của cạnh BC. Tính độ dài đoạn thẳng MA
Bài 15: Cho tam giác ABC vuông tại A, có AC = 20 cm; AB = 15 cm. Gọi M là trung điểm của cạnh BC. Tính độ dài đoạn thẳng MA.
a) ABC có
MA = MB ( gt )
NB = NC ( gt )
=> MN là đường trung bình của ABC
=> MN = AC =
.20 = 10 ( cm )
vuông tại A
=>
=>
= 25 cm
có
AN là đường trung tuyến ( NB = NC )
=> AN = =
= 12,5 ( cm ))
b) ABDC có 2 đường chéo AD , BC cắt nhau tại N
mà CN = ND ( gt )
AN = ND ( gt )
=> ABDC là hình bình hành
mà
=> ABDC là hình chữ nhật
*(Cho mình 1 nút like vs bn ơi )
Đúng 0
Bình luận (0)
Bài 15: Cho tam giác ABC vuông tại A, có AC = 20 cm; AB = 15 cm. Gọi M là trung điểm của cạnh BC. Tính độ dài đoạn thẳng MA
Cho tam giác ABC có B A C ^ > 90 ° . Kẻ AH vuông góc với BC tại H. Biết AB = 15 cm; AC = 41 cm, BH = 12 cm. Tính độ dài cạnh HC.
cho tam giác ABC vuông tại A . Có AB bằng 6 cm. AC bằng 8 cm. a tính độ dài cạnh BC và chu vi tam giác ABC . Đường phân giác của góc B cắt AC tại D .Vẽ DH vuông góc BC . [ H thuộc BC ]. CM tam giác ABD = tam giác HBD c CM DA < DC . có vẽ hình nha mọi người
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
Đúng 2
Bình luận (0)
tam giác ABC vuông tại A có chu vi 120 cm.Độ dài AC lớn hơn độ dài AB 10 cm. Cạnh BC dài 50 cm. Tính: a) Độ dài cạnh AB, AC b) Diện tích tam giác c) Độ dài đường cao AH
a) Nửa chu vi tam giác là :
\(120\div2=60\left(cm\right)\)
Độ dài đáy AC là :
\(\left(60+10\right)\div2=35\left(cm\right)\)
Độ dài đáy AB là :
\(60-35=25\left(m\right)\)
b) Chiều cao AH là :
\(60-50=10\left(m\right)\)
c) Diện tích tam giác là :
Đúng 2
Bình luận (1)
a) Tổng độ dài AC, AB là:
\(120-50=70\left(cm\right).\)
Độ dài AC là: \(\dfrac{\left(70+10\right):2}{2}=40\left(cm\right).\)
Độ dài AB là: \(70-40=30\left(cm\right)\)
b) Diện tích tam giác ABC là: \(\dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times30\times40=600\left(cm^2\right).\)
c) Độ dài đường cao AH là: \(600:\dfrac{1}{2}:BC=600:\dfrac{1}{2}:50=24\left(cm\right).\)
Đúng 0
Bình luận (0)
nãy tôi thử ae thôi :>
Theo bài ra ta có : AB + AC + BC = 120
<=> AB + AC = 70 (1)
Lại có : AC - AB = 10 (2)
Từ (1) ; (2) suy ra :
\(\left\{{}\begin{matrix}AB+AC=70\\-AB+AC=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2AC=80\\AB=AC-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=40\\AB=30\end{matrix}\right.\)
b, Diện tích tam giác là : \(S=\dfrac{1}{2}.AC.AB=\dfrac{1}{2}.40.30=600cm^2\)
c, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức :
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{1200}{50}=\dfrac{120}{5}=24cm\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, AC = 8 cm, AB = 6 cm và tam giác HIK vuông tại H, HI = 15 cm, IK = 25 cm
a) Tính độ dài BC, HK
b) Hai tam giác ABC và HIK có đồng dạng vs nhau k? Vì sao?
điểm H,K,I ở chỗ nào vậy