a, Ta có ∆ABE = ∆ADF(g.c.g) => AE = AF

b, Ta có: ∆AKF ~ ∆CAF ( F ^ chung và  F A K ^ = F C A ^ = 45 0 )

=> A F H F = C F A F =>  A F 2 = K F . C F

c, S A E F = 93 2 c m 2

d, Ta có: AE.AJ=AF.AJ=AD.FJ

=>  A E . A J F J = AD không đổi

b, Vì ∆ABD=∆EBD

=>BAD=BED=90°

=>DE//BC

Ta có AH vuông góc BC

DE vuông góc BC

=>AH//DE(đpcm)

c,Đó AH//DE (đpcm)

=>AH//DK.

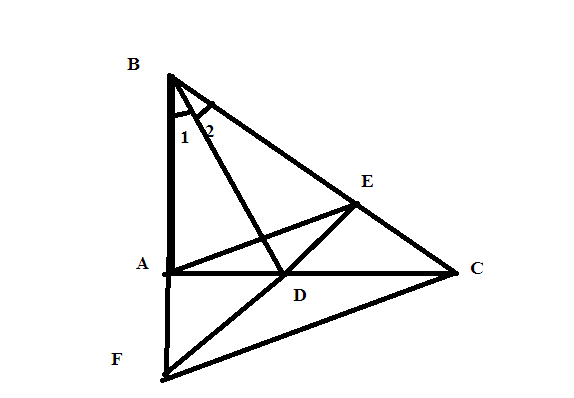
Xét ΔBAD và ΔBDE có:

BD là cạnh chung

B₁=B₂ (BD là tia phân giác của \(\widehat{B}\))

BA = BE (GT)

Nên ΔBAD= ΔBDE (c.g.c)

=>\(\widehat{ADB}=\widehat{BDE}\)

Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)

         \(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)

Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)

        \(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)

=>\(\widehat{BDF}=\widehat{BDC}\)

Xét ΔBDF và Δ BDC, có:

\(\widehat{BDF}=\widehat{BDC}\)

BD là cạnh chung

B₁=B₂

Nên ΔBDF=ΔBDC (g.c.g)

=>DC = DF

b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE

MÀ DE=AD (ΔBAD và ΔBDE)

=> AD< DC

c) Ta có BE=BA=>ΔBEA cân tại B

Mà BD là tia phân giác=>BD là đường trung trực

Vì :ΔBDF=ΔBDC=>BF=BC 

=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)

Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)

=>\(\widehat{B}+\widehat{C}.2=180^O\)

=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)

vÌ ΔBAE  cân tại B

Tương tự ta có:

\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)

Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)

Mà 2 góc này ở vị trí đồng vị=>AE // FC

a: Xét ΔABC có AD/AB=AE/AC

nên DE//BC

b: Xét ΔABI có DM//BI

nên DM/BI=AD/AB

Xét ΔACI có EM//IC

nên EM/CI=AE/AC

=>DM/BI=EM/CI

=>DM=EM

=>M là trung điểm của DE

c: AI là phân giác

=>IB/IC=AB/AC=AD/AE

=>IB*AE=IC*AD