325253737747⁸⁹⁰⁷⁶⁵⁴³ chuyển đổi sang STN là?

1, để \(\dfrac{2x+1}{x+3}\) là 1 số nguyên 

= > 2x + 1 chia hết cho x + 3 ( x thuộc Z và x \(\ne3\) )

= > 2 ( x + 3 ) - 5 chia hết cho x + 3 

=> -5 chia hết cho x + 3 

hay x + 3 thuộc Ư(-5 ) \(\in\left\{\pm1;\pm5\right\}\)

Đến đây em tự tìm các giá trị của x

2, Tương tự câu 1, x - 1 chia hết cho x + 5 ( x thuộc Z và x khác - 5 )

= > - 6 chia hết cho x + 5 

= > \(x+5\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)

....

3,  ( x - 1 ) ( y - 3 ) = 7 

x,y thuộc Z = > x - 1 ; y - 3 thuộc Ư(7)

và ( x - 1 )( y - 3 ) = 7

( 1 ) \(\left\{{}\begin{matrix}x-1=1\\y-3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=10\end{matrix}\right.\)

(2) \(\left\{{}\begin{matrix}x-1=7\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)

( 3) \(\left\{{}\begin{matrix}x-1=-1\\y-3=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\)

( 4 ) \(\left\{{}\begin{matrix}x-1=-7\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\)

Từ ( 1 ) , ( 2 ) , ( 3 ) , ( 4 ) các cặp giá trị ( x,y ) nguyên cần tìm là ....

kho nhi

Tham khảo tại đây nhé bạn:

Câu hỏi của Trang Huyen Trinh - Toán lớp 6 - Học toán với OnlineMath

Câu hỏi của Trang Huyen Trinh - Toán lớp 6 - Học toán với OnlineMath

Câu hỏi của Trang Huyen Trinh - Toán lớp 6 - Học toán với OnlineMath

https://olm.vn/hoi-dap/detail/4066749213.html

Xét x=0,x=1 thì thỏa mãn

Xét x khác 0,1

Dùng phản chứng là ra mà "<<

Với mọi số nguyên n ta có n <= n² . Do đó từ đề bài suy ra :

    x² <= y <= y² <= z <= z² <= x <= x².

Do đó x^2 = y = y^2 = z = z^2 = x = x^2.

Ta có : x^2 = x <=> x(x-1) = 0 <=> x = 0 và x = 1

Tương tự như thế

Vậy : ...

\(0\le\left|x\right|\le3\)      \(0\le\left|y\right|\le5\)     \(x-y=2\)
Vì \(x-y=2\Rightarrow x=y+2\)\(\Rightarrow0\le\left|y+2\right|\le3\Rightarrow0\le\left|y\right|\le1\)
\(\Rightarrow\left|y\right|=\orbr{\begin{cases}1\\0\end{cases}}\)\(\Rightarrow y=\orbr{\begin{cases}\orbr{\begin{cases}1\\-1\end{cases}}\\0\end{cases}\Rightarrow x=\orbr{\begin{cases}\orbr{\begin{cases}4\\2\end{cases}}\\3\end{cases}}}\)\(\Rightarrow y=\left(-1;0;1\right)\Rightarrow x=\left(1;2;3\right)\)
\(\left(x;y\right)=\left(-1;1\right),\left(0;2\right),\left(1;3\right)\)

\(\hept{\begin{cases}!x!\le3\\!y!\le5\\x-y=2\end{cases}}\Rightarrow\hept{\begin{cases}-3\le x\le3\\-5\le y\le5\\y=x+2\end{cases}}\)

với x={-3,-2,-1,0,1,2,3}

=> y={-1,0,1,2,4,5}

\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)

Đặt \(\dfrac{x}{y}=t\)

\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)

Với \(P=0\Leftrightarrow t=2\)

Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)

\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)

Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)

\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)

Bài a hình như sai đề rồi bạn.

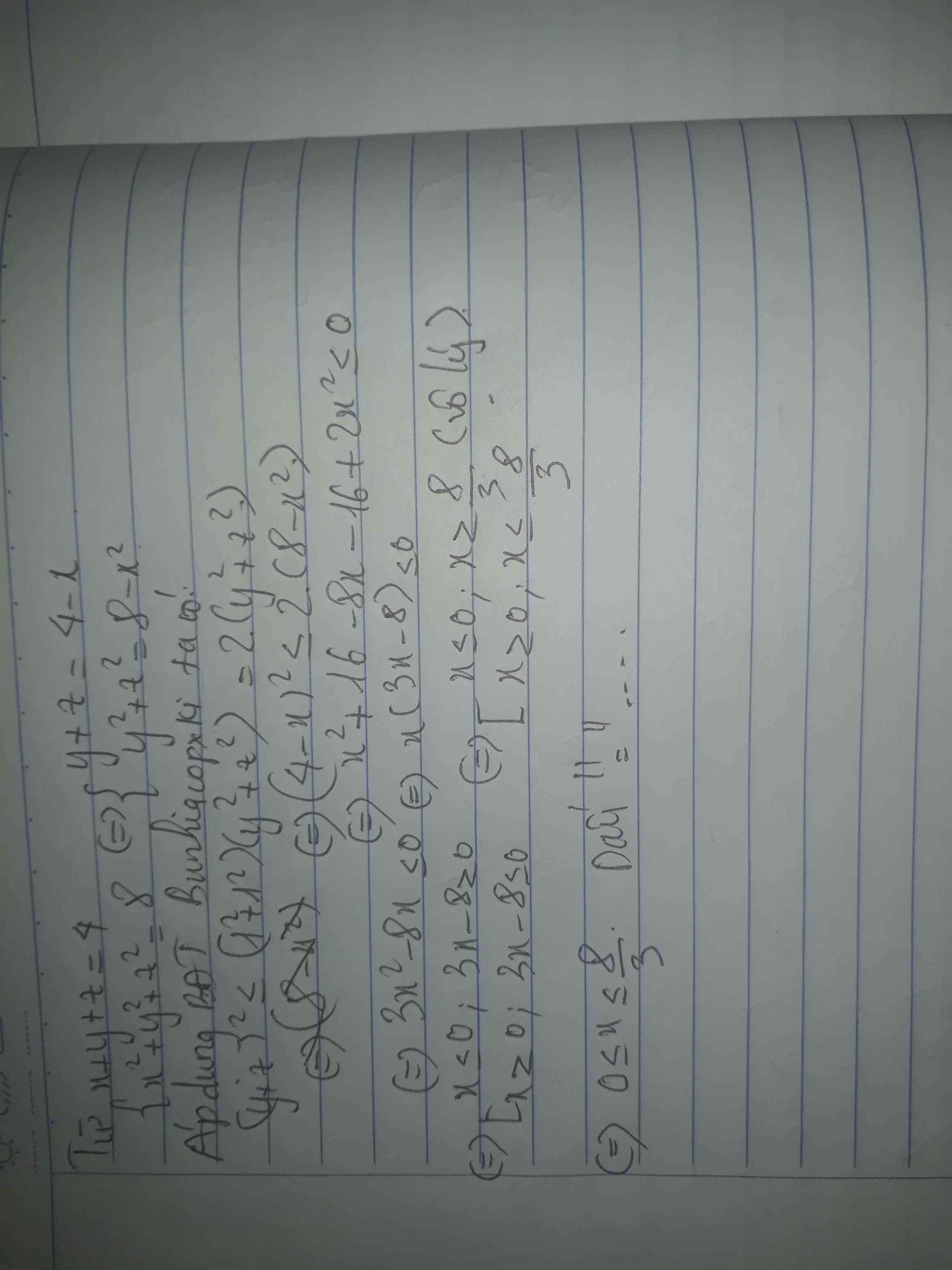
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)

Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)