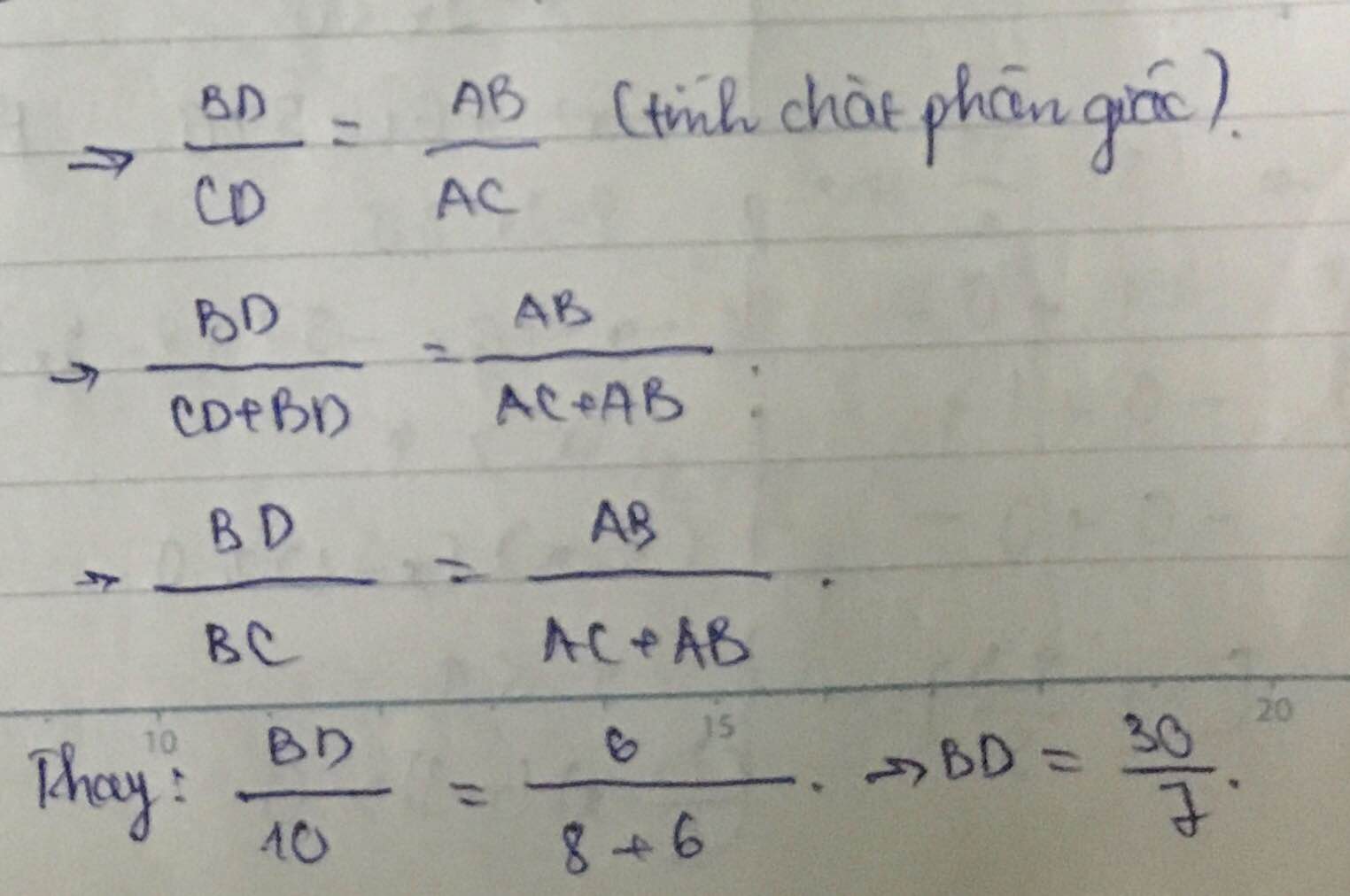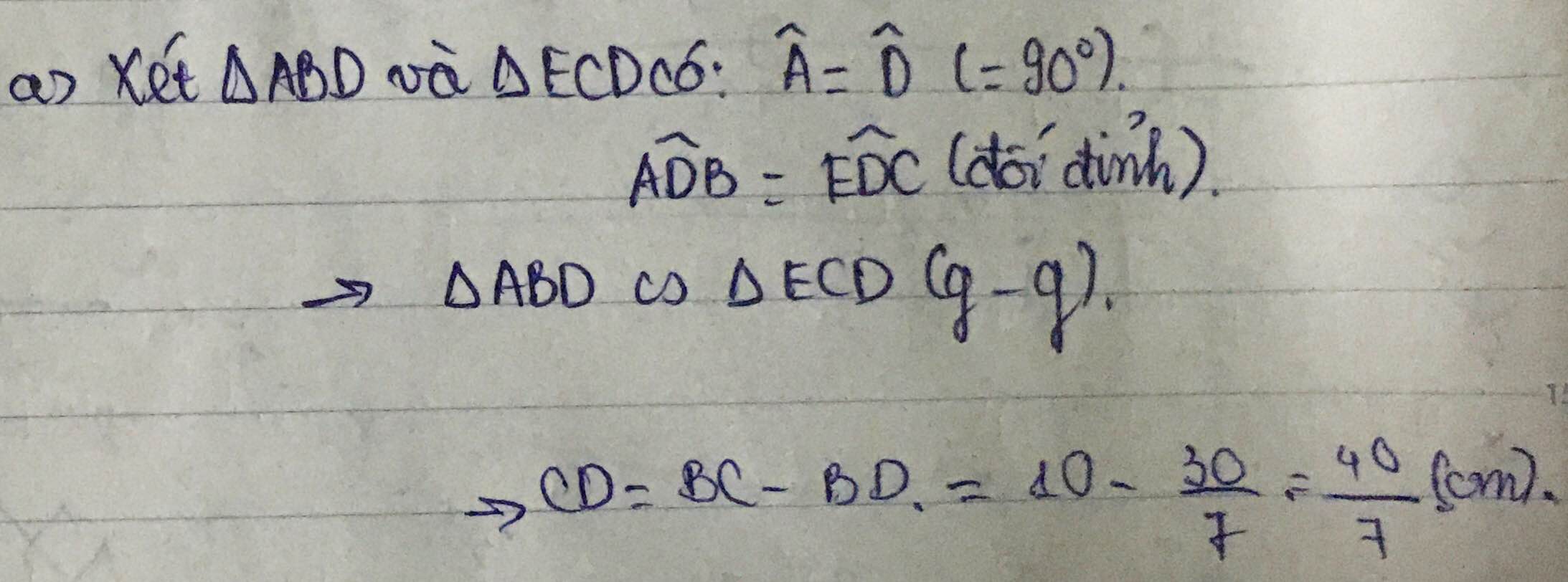Cho tam giác OCD vuông tại O, biết OC = 6cm, OD = 8cm. Tính độ dài CD.
Những câu hỏi liên quan
1. Cho tam giác OCD vuông tại O có đường cao OH. Biết CD = 24cm , .
Tính độ dài OH, OC, OD.
2. Cho tam giác DEF vuông tại D, đường cao DI. Biết , DE = 18 cm . Giải tam giác DEF và tính độ dài DI.
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
\(DH=15\left(cm\right)\)
\(OC=\sqrt{9\cdot24}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
\(OH=3\sqrt{15}\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác OCD vuông tại O có OC=6cm;OD=8cm Trên cạnh OC lấy điểm B sao cho OB = 4 cm trên cạnh OD lấy điểm A sao cho OA=3cm. a) Chứng minh rằng: tam giác OAB đồng dạng với tam giác OCD b) Qua C kẻ CE/AB (E thuộc OD). Tính CE ? c) Chứng minh rằng: OC^2= OD.OE
Bài 1Cho tam giác OCD vuông tại O có đường cao OH. Biết CD 24cm , HC/HD3/5 . Tính độ dài OH, OC, OD. Bài 2Cho tam giác DEF vuông tại D, đường cao DI. Biết DF/EF4/5 , DE 18 cm . Giải tam giác DEF và tính độ dài DI.
Đọc tiếp
Bài 1
Cho tam giác OCD vuông tại O có đường cao OH. Biết CD = 24cm , HC/HD=3/5 . Tính độ dài OH, OC, OD.
Bài 2
Cho tam giác DEF vuông tại D, đường cao DI. Biết DF/EF=4/5 , DE = 18 cm . Giải tam giác DEF và tính độ dài DI.
Bài 1:
\(CH=24\cdot\dfrac{3}{8}=9\left(cm\right)\)
DH=15(cm)
\(OH=3\sqrt{15}\left(cm\right)\)
\(OC=\sqrt{OH^2+CH^2}=\sqrt{81+135}=6\sqrt{6}\left(cm\right)\)
\(OD=\sqrt{24^2-216}=6\sqrt{10}\left(cm\right)\)
Đúng 0
Bình luận (0)
cho hình thang vuông ABCD có góc A= góc D= 90° và hai đường chéo vuông góc với nhau tại O. a) CM: tam giác OAB= tam giác OCD. b) CM: tam giác ABD và tam giác ACD đồng dạng với nhau. c) Tính diện tích tam giác OAB biết AD=6cm,CD=8cm
a: Xét ΔOAB vuông tại O và ΔOCD vuông tại O có
góc OAB=góc OCD
=>ΔOAB đồng dạng với ΔOCD
b: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
Đúng 0
Bình luận (0)
Cho tam giác OCD vuông tại O, đường cao OK, biết OC = 15cm, OD = 20cm.
Vẽ CE là phân giác của góc OCD. Gọi M là giao điểm của OK và CE. Chứng minh tam giác OME cân
Ta có: \(\widehat{CMK}+\widehat{ECD}=90^0\)(ΔCKM vuông tại K)
\(\widehat{CEO}+\widehat{OCE}=90^0\)(ΔCOE vuông tại O)
mà \(\widehat{ECD}=\widehat{OCE}\)(CE là phân giác của góc OCD)
nên \(\widehat{CMK}=\widehat{CEO}\)
mà \(\widehat{CMK}=\widehat{OME}\)(hai góc đối đỉnh)
nên \(\widehat{OME}=\widehat{OEM}\)
=>ΔOEM cân tại O
Đúng 0
Bình luận (0)
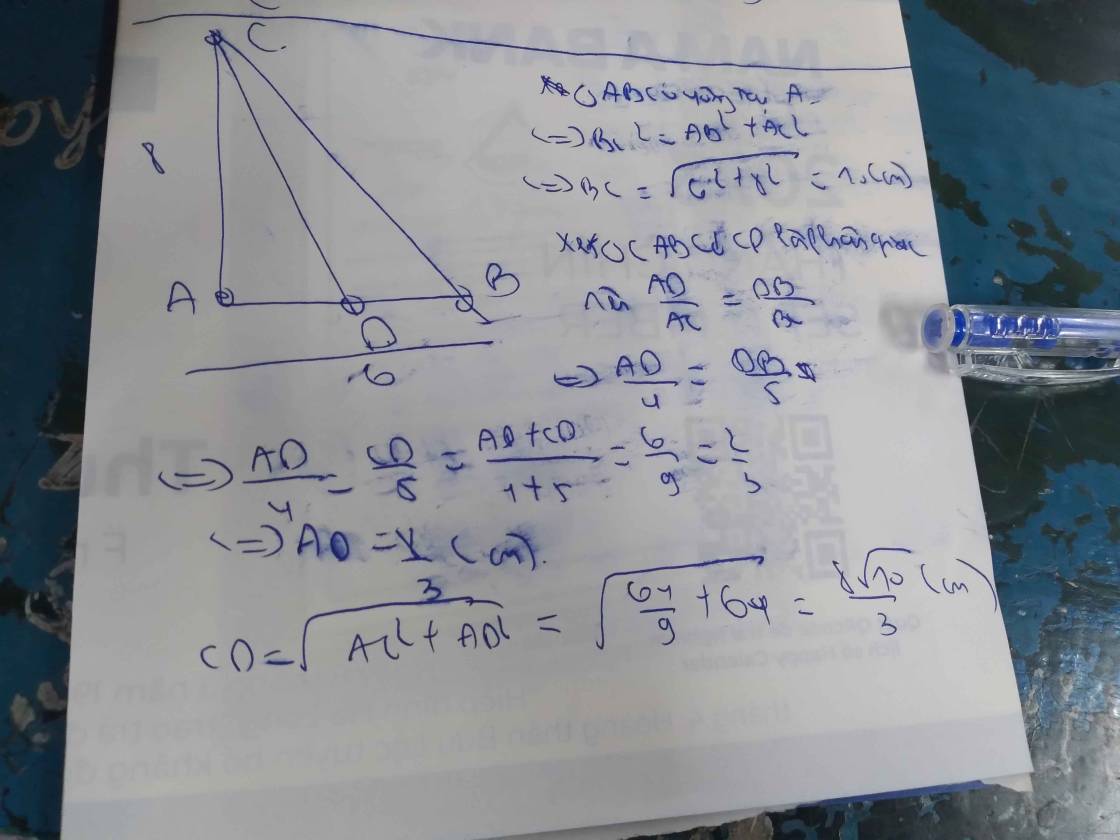
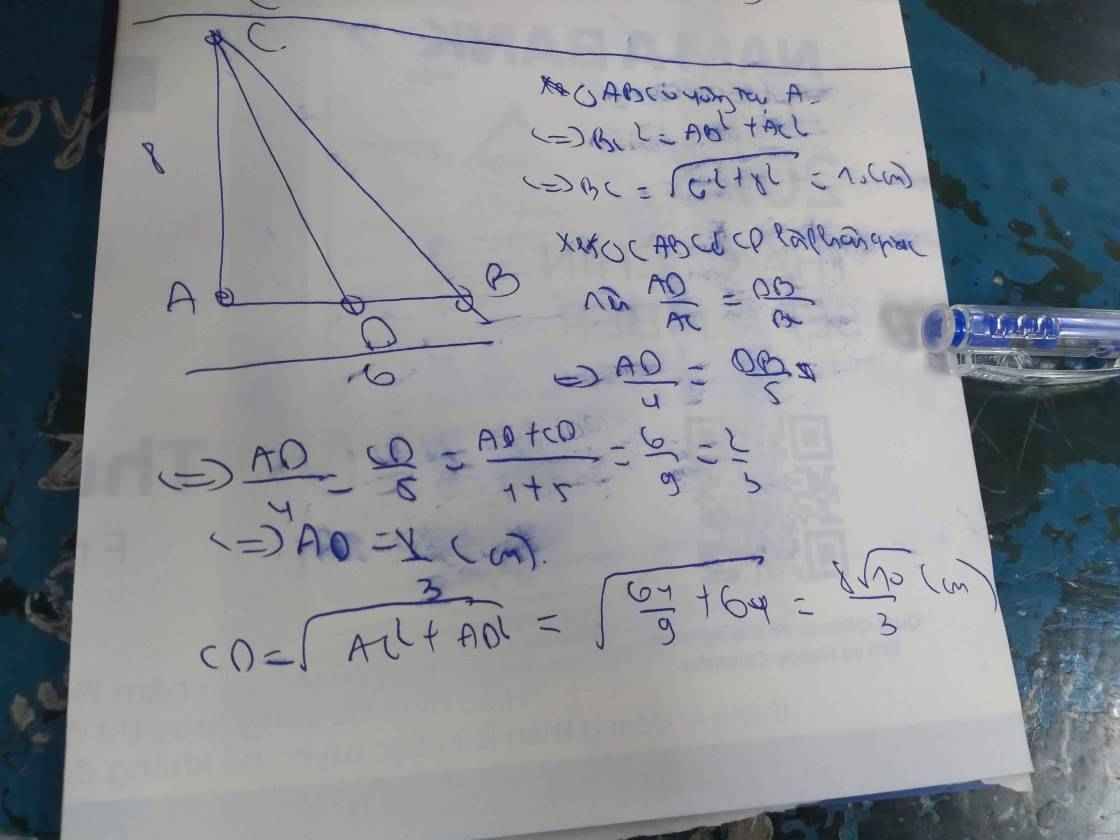
Cho tam giác ABC vuông tại A có AB=6cm; AC= 8cm. Tính độ dài đường phân giác trong CD
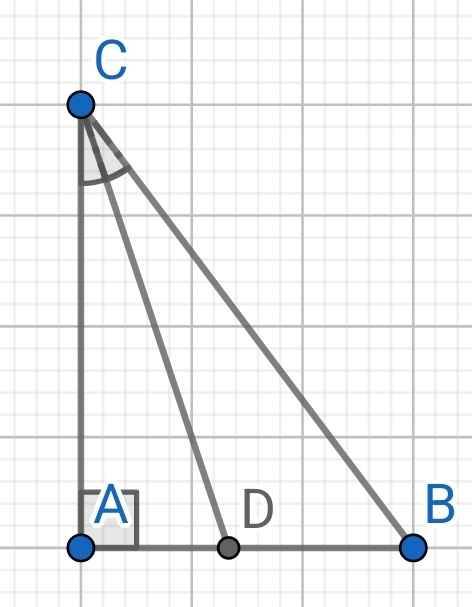Do ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC.1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AC² + AD² (Pytago)
= 8² + (8/3)²
= 640/9
⇒ CD = 8√10/3 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB=6cm và AC= 8cm. Tính độ dài đường phân giác trong CD
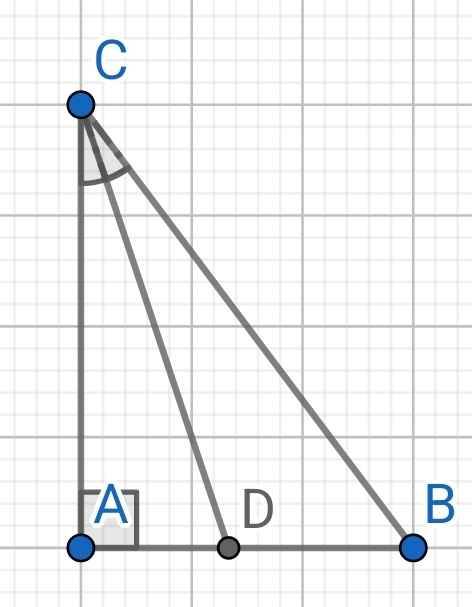∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác của ∆ABC (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC . 1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AD² + AC² (Pytago)
= (8/3)² + 8²
= 640/9
⇒ CD = 8√10/3 (cm)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC =8cm. Phân giác AD.
a)Tính độ dài BD và CD b) Kẻ DH vuông góc với AB. Tính DH, AD .
Cho hình thang cân ABCD (AB//CD) có AC vuông góc với BD tại O.
a) Chứng minh các tam giác OCD, OAB vuông cân.
b) Biết AB = 2cm, CD = 8cm, AD = 5cm. Tính diện tích hình thang ABCD.
. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2
Đúng 0
Bình luận (0)