Phương pháp giải:

 Vận dụng kiến thức về ba điểm thẳng hàng, vẽ theo yêu cầu của bài toán.

Lời giải chi tiết:

a) Đi qua hai điểm M, N

Chấm thêm một điểm P để M, N, P thẳng hàng.

b) Đi qua điểm O

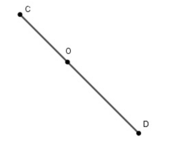
Chấm thêm 2 điểm C và D để C, O, D thẳng hàng.

c) Đi qua hai trong ba điểm A, B, C.

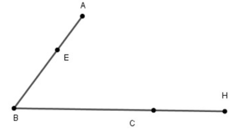
Chấm thêm hai điểm E và H để A, E, B thẳng hàng và B, C, H thẳng hàng.

Vì (d) đi qua M(1;3) và N(-2;0) nên ta có hệ:

a+b=3 và -2a+b=0

=>a=1; b=2

=>y=x+2

Thay x=-1/2 và y=3/2 vào (d), ta được;

2-1/2=3/2(luôn đúng)

=>M,N,E thẳng hàng

a/

\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)

b/

Tọa độ A là \(A\left(x_0;y_0\right)\)

\(\Rightarrow y_0=4mx_0-m-5\forall m\)

\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)

=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)

Tọa độ B là \(B\left(x_1;y_1\right)\)

\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)

\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)

\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)

=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)

d/ d1//d2 khi

\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)

Ta có \(m^2+m+1>0\forall m\)

\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)

e/

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm

Tìm giao

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2

Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y