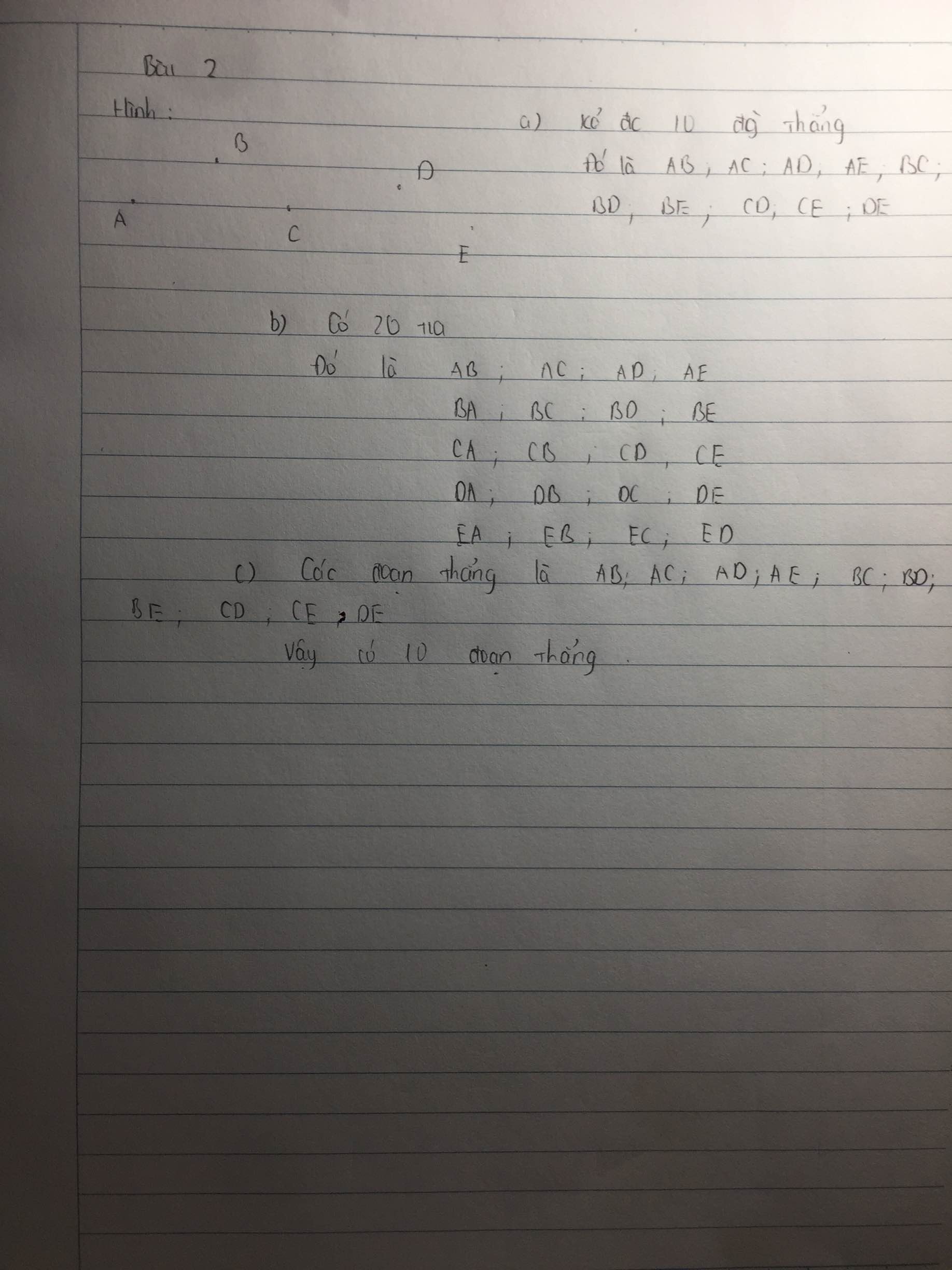\(x^4-8x=x\left(x^3-8\right)=x\left(x-2\right)\left(x^2+2x+4\right)\)

\(x^2-y^2-6x+9=\left(x^2-6x+9\right)-y^2=\left(x-3\right)^2-y^2=\left(x+y-3\right)\left(x-y-3\right)\)

Chắc là biến đổi trong bài tìm pt mặt phẳng

Từ hệ 2 pt đầu ta rút ra được: \(\left\{{}\begin{matrix}c=-a-b\\d=2a+b\end{matrix}\right.\)

Thế vào pt cuối:

\(\dfrac{\left|3a-b\right|}{\sqrt{a^2+b^2+\left(a+b\right)^2}}=\dfrac{3}{\sqrt{2}}\)

\(\Rightarrow2\left(3a-b\right)^2=9\left(a^2+b^2\right)+9\left(a+b\right)^2\)

\(\Rightarrow15ab+8b^2=0\Rightarrow\left[{}\begin{matrix}b=0\\b=-\dfrac{15a}{8}\end{matrix}\right.\)

Câu 1.

Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)

\(;a_i\ne a_j\)

Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.

5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)

\(\Rightarrow\)Có \(A_8^5\) cách.

Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.

c

Sửa đề: \(\dfrac{1}{1.9}\rightarrow\dfrac{9}{9.19}\)

Giải:

\(N=\dfrac{9}{9.19}+\dfrac{9}{19.29}+\dfrac{9}{29.39}+...+\dfrac{9}{2019.2029}\) 

\(N=\dfrac{9}{10}.\left(\dfrac{10}{9.19}+\dfrac{10}{19.29}+\dfrac{10}{29.39}+...+\dfrac{10}{2019.2029}\right)\) 

\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{2019}-\dfrac{1}{2029}\right)\) 

\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{2029}\right)\) 

\(N=\dfrac{9}{10}.\dfrac{2020}{18261}\) 

\(N=\dfrac{202}{2029}\)

mn giúp e với ạ

a: 2+5/6=12/6+5/6=17/6

b: 5/12+3/4+1/3=5/12+9/12+4/12=18/12=3/2

c: 2/3+3/4=8/12+9/12=17/12

a) Vì ABCD là hình bình hành ( gt )

⇒ AD // BC 

      F ∈ BC

⇒ AD // BF

⇒ ∠EDA = ∠EFB ( hai góc so le trong )

Xét △AED và △BEF, có :

∠EDA = ∠EFB ( cmt )

∠AED = ∠FEB ( hai góc đối đỉnh )

⇒ △AED ∼ △BEF (g-g)

b) Vì ABCD là hình bình hành ( gt )

⇒ AB // CD 

      E ∈ AB

⇒ BE // CD

Xét △FDC, có :

BE // CD ( cmt )

E ∈ DF ; B ∈ DC 

⇒ \(\dfrac{FB}{FC}=\dfrac{EB}{DC}\) (Hệ quả của định lí Ta-let)

⇒ \(\dfrac{BF}{BE}=\dfrac{FC}{DC}\) (1)

Vì △AED ∼ △BEF ( cmt )

⇒ \(\dfrac{AE}{BE}=\dfrac{AD}{BF}\) (TSDD)

⇒ \(\dfrac{AE}{AD}=\dfrac{BE}{BF}\) (2)

Từ (1) và (2) ⇒ \(\dfrac{AE}{AD}=\dfrac{CF}{CD}\)

⇒ AD.CD = AE.CF

c) Xét △DGC, có : 

AE // DC ( cmt )

G ∈ AC ; G ∈ DE

⇒ \(\dfrac{DG}{DE}=\dfrac{GC}{AC}\) (Hệ quả của định lí Ta-let) (3)

Xét △FGC, có : 

AD // CF ( cmt )

G ∈ AC ; G ∈ DF

⇒ \(\dfrac{DG}{DF}=\dfrac{AG}{AC}\) (Hệ quả của định lí Ta-let) (4)

Từ (3) và (4) ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}=\dfrac{GC}{AC}+\dfrac{AG}{AC}\)

                     ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}\)  =  1

                     ⇒  \(\dfrac{1}{DG}\left(\dfrac{DG}{DE}+\dfrac{DG}{DF}\right)=\dfrac{1}{DG}\)

                     ⇒  \(\dfrac{1}{DG}=\dfrac{1}{DE}+\dfrac{1}{DF}\)