Nó là điểm Q

Đơn giản là kĩ năng đọc đường tròn lượng giác

\(\dfrac{7\pi}{4}\) thì từ gốc A quay theo chiều kim đồng hồ 1 góc 45 độ sẽ được \(\dfrac{7\pi}{4}\)

Đề bài là gì thế bạn?

đề kìa :

X⁴ + 2x³ + 5x² + 4x - 12 = ?

Đây là phân tích đa thức thành nhân tử = phương pháp đặt biến phụ ạ

Bài 1:

3: ĐKXĐ: x>=1

\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)

=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)

=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)

=>\(x-\left|\sqrt{x-1}+2\right|=1\)

=>\(x-\left(\sqrt{x-1}+2\right)=1\)

=>\(x-\sqrt{x-1}-2-1=0\)

=>\(x-1-\sqrt{x-1}-2=0\)

=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)

=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)

=>\(\sqrt{x-1}-2=0\)

=>\(\sqrt{x-1}=2\)

=>x-1=4

=>x=5(nhận)

Bài 1:

a. \(=2\sqrt{3^2}+\sqrt{15}-\sqrt{4.15}=6+\sqrt{15}-2\sqrt{15}=6-\sqrt{15}\)

b. \(=5\sqrt{10}+2\sqrt{5^2}-\sqrt{25.10}=5\sqrt{10}+10-5\sqrt{10}=10\)

c. \(=\left(\sqrt{4.7}-\sqrt{4.3}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)

\(=2\sqrt{7^2}-2\sqrt{21}-\sqrt{7^2}+2\sqrt{21}=7\)

d. \(=\left(\sqrt{9.11}-\sqrt{9.2}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)

\(=\left(3\sqrt{11}-3\sqrt{2}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)

\(=3\sqrt{11^2}-3\sqrt{22}-\sqrt{11^2}+3\sqrt{22}=22\)

Bài 3:

a.

\(=\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+\sqrt{x}^2\right)=1-\sqrt{x}^3=1-x\sqrt{x}\)

b.

\(=\left(\sqrt{x}+2\right)\left(\sqrt{x}^2-2\sqrt{x}+2^2\right)=\sqrt{x}^3+2^3=x\sqrt{x}+8\)

c.

\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}^2+\sqrt{xy}+\sqrt{y}^2\right)=x\sqrt{x}-y\sqrt{y}\)

d.

\(=\left(x+\sqrt{y}\right)\left(x^2-x\sqrt{y}+\sqrt{y}^2\right)=x^3+y\sqrt{y}\)

\(d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)=\dfrac{a}{2}\)

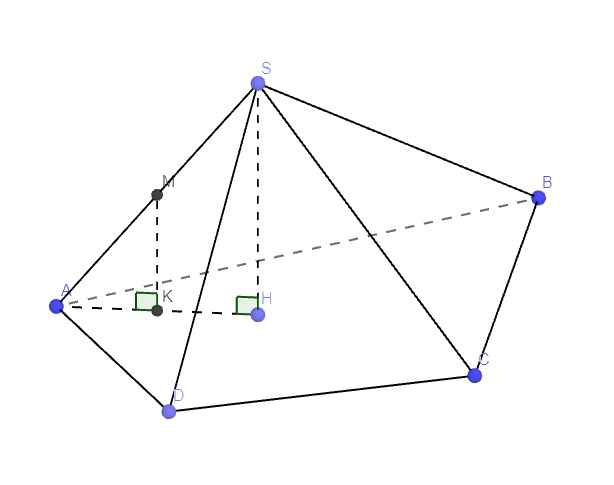
Theo định lý Talet ta luôn có: 

\(\dfrac{MK}{SH}=\dfrac{AM}{SA}=\dfrac{1}{2}\Rightarrow MK=\dfrac{1}{2}SH\)

Hay \(d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)\)