a) Xét tam giác ABM và tam giác ACM:

+ AM chung.

+ AB = AC (gt).

+ \(\widehat{ABM}=\widehat{ACM}\) (AM là phân giác \(\widehat{BAC}\) ).

\(\Rightarrow\) Tam giác ABM = Tam giác ACM (c - g - c).

b) Xét tam giác ABC: AB = AC (gt).

\(\Rightarrow\) Tam giác ABC cân tại A.

Mà AM là phân giác \(\widehat{BAC}\) (gt).

\(\Rightarrow\) AM là trung tuyến (Tính chất tam giác cân).

\(\Rightarrow\) M là trung điểm của BC.

là tam giác cân

bài này thiếu 1 điều kiện bạn  xem lại đi nha

có thêm điều kiện thiếu giải đã khó chứu ko  ns đến giải thiếu hẳn ntn.

Bạn xem lại mik làm bài này nhiều nên biết.mik thuộc đề bài mà 

Từ M kẽ MH vuông góc với AB , MK vuông góc với AC

Xét 2 \(\Delta\) vuông AMH và AMK có:

           góc HAM = góc KAM (AM là tia phân giác của góc BAC)

                  AM chung

\(\Rightarrow\Delta AMH=\Delta AMK\left(ch-gn\right)\)

\(\Rightarrow MH=MK\)( 2 cạnh tương ứng)

  Xét 2 \(\Delta\) vuông BHM và CKM có:

           MH = MK (cmt)

           BM = MC ( M là trung điểm của BC)

\(\Rightarrow\Delta BHM=\Delta CKM\left(ch-cgv\right)\)

\(\Rightarrow\) góc B = góc C ( 2 góc tương ứng)

\(\Rightarrow\) \(\Delta ABC\) cân tại A

a: Xet ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔABC cân tại A

mà AM là trung tuyến

nên AM là đường cao

BC=12cm nên BM=6cm

=>AM=8(cm)

c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác

=>AI là phân giác của góc BAC

mà AM là phân giác của góc BC

nên A,I,M thẳng hàng

a, Xét tam giác AMB và tam giác AMC có

AB = AC (gt)

AM chung

MB = MC ( M là trung điểm BC )

=> tam giác AMB = tam giác AMC (c.c.c)

=>\(\widehat{BAM}=\widehat{CAM}\)

=> AM là phân giác góc BAC

b, Vì tam giác AMB = tam giác AMC (cmt)

\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)

Ta có : \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)

\(\Rightarrow\widehat{AMB}+\widehat{AMB}=180^o\)

\(\Rightarrow\widehat{AMB}=90^o\)

\(\Rightarrow AM\perp BC\left(ĐPCM\right)\)

a) Xét tam giác ABC có : AB = AC 

=> Tam giác ABC cân tại A

Mà AM là đường trung tuyến ứng với BC ( vì M là trung điểm của BC) 

=>AM vừa là đường trung tuyến đồng thời là đường phân giác 

Do đó : AM là tia phân giác của góc BAC(đpcm)

b)Vì tam giác ABC cần tại A ( theo câu a ) 

Nên đường phân giác AM đồng thời là đường cao 

=> AM vuông góc với BC ( đpcm )

Nếu thấy đúng cho mình 1  

a: Xét tứ giác ABCE có

D là trung điểm của AC

D là trung điểm của BE

Do đó; ABCE là hình bình hành

Suy ra: BC//AE

b: Xét ΔABC có 

AM là đường trung tuyến

BD là đường trung tuyến

AM cắt BD tại I

Do đó: I là trọng tâm của ΔABC

a: OM//AH

ON//BH

MN//AB

=>góc BAH=góc OMN và góc ABH=góc ONM

=>ΔABH đồng dạng với ΔMNO

b: A,G,M thẳng hàng và H,G,O thẳng hàng

=>góc AGH=góc MGO

=>ΔAHG đồng dạng với ΔMOG

=>OM/AH=MG/AG

=>OM/AH=MN/AB=1/2

=>GM/GA=1/2

=>G là trọng tâm của ΔACB

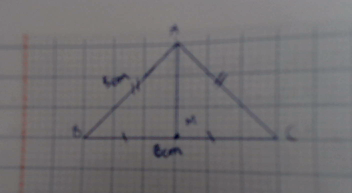 cam máy tính hình nó mờ nha bạn 

a) Xét ΔAMB và ΔAMC ta có:

AB=AC ( tích chất tam giác cân)

AM=MC (giả thiết)

AM cạnh chung

⇒ ΔAMB = ΔAMC (c-c-c)

⇒ \(\widehat{AMB}=\widehat{AMC}\) (hai góc tương ứng), mà hai góc này kề bù nên

\(\widehat{AMB}=\widehat{AMC}=\dfrac{180}{2}=90^o\)

Vậy AM ⊥ BC (đpcm) 

b) từ câu a ta có  ΔAMB = ΔAMC nên:

\(\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)

⇒ AM là tia phân giác của \(\widehat{BAC}\)  (đpcm)

c) Ta có AM ⊥ BC (1)

             BM=CM (2) vì AM vuông góc với BC và M cách đều BC (BM=CM) 

từ (1) và (2) ⇒  AM là đường trung trực của AB

s ít thấy xu on hoc24 nhỉ?