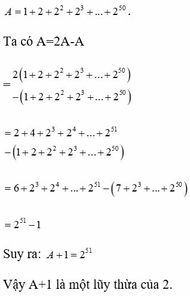Cho A = 4+22 +23+24+25+...+22002.Chứng minh rằng A là một lũy thừa của 2

Những câu hỏi liên quan
Cho A 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2.
Đọc tiếp
Cho A = 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2.
A=4+22+23+....+220
2A=8+23+24+...+221
=> A+2A-A = (8+23+24+...+221) - (4+22+23+....+220)
=>A=221+8 - (22+4)=221
=>A là 1 lũy thừa của 2
Đúng 0
Bình luận (0)
Cho A = 4 + 22 + 23 + 24 + ... + 22002. Chứng minh rằng A là một luỹ thừa của 2
A= 4+22+23+....+220
2A= 8+23+24+...+221
A + 2A -A = (8+2^3+2^4+...+2^21) - (4+2^2+2^3+....+2^20)
A= 2^21+8 - (2^2+4)=2^21
Vậy A là 1 lũy thừa của 2
Đúng 1
Bình luận (0)
Cho A=4+22+23+24+...+22002.Chứng minh rằng A là một luỹ thừa của 2
Giúp đi nhanh k cho
Cho A=4+22+23+24+...+22002. Chứng minh rằng A là một luỹ thừa của 2
giúp với nhanh kich cho
vậy nên mình mới hỏi chứ bỏ 23 đi thì mình tự giải cũng đc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho A=4+23+24+25+...+220
chứng minh rằng A là một lũy thừa của 2
\(A=4+2^3+2^4+2^5+...+2^{20}\)
\(A=2^2+2^3+2^4+2^5+...+2^{20}\)
\(\Rightarrow2A=2^3+2^4+2^5+2^6+...+2^{21}\)
\(\Rightarrow2A-A=\left(2^3+2^4+2^5+2^6+...+2^{21}\right)-\left(2^2+2^3+2^4+2^5+...+2^{20}\right)\)
\(\Rightarrow A=2^{21}-2^2\)
\(=2^2\left(2^{19}-1\right)\)
Vậy A là một lũy thừa của 2.
#kễnh
Đúng 3
Bình luận (1)
A= 4 + 22 + 23 + ... + 22006
Chứng minh rằng A là 1 lũy thừa của cơ số 2
\(A=4+2^2+2^3+...+2^{2006}\)
\(\mathsf{Đặt}:B=2^2+2^3+...+2^{2006}\\2B=2^3+2^4+...+2^{2007}\\2B-B=(2^3+2^4+...+2^{2007})-(2^2+2^3+...+2^{2006})\\B=2^{2007}-2^2\\B=2^{2007}-4\)
Thay \(B=2^{2007}-4\) vào A, ta được:
\(A=4+(2^{2007}-4)\\\Rightarrow A=2^{2007}\)
$\Rightarrow A$ là 1 luỹ thừa của cơ số 2.
Vậy: ...
Đúng 3
Bình luận (0)
Cho A
1
+
2
+
2
2
+
2
3
+
.
.
.
+
2
50
. Chứng tỏ rằng: A + 1 là một lũy thừa của 2
Đọc tiếp
Cho A = 1 + 2 + 2 2 + 2 3 + . . . + 2 50 . Chứng tỏ rằng: A + 1 là một lũy thừa của 2
Ta có A = 2A – A = 2( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 2 + 4 + 2 3 + 2 4 + . . . + 2 51 – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 6 + 2 3 + 2 4 + . . . + 2 51 – ( 7 + 2 3 + . . . + 2 50 ) = 2 51 - 1
Suy ra : A + 1 = 2 51
Vậy A+1 là một lũy thừa của 2
Đúng 0
Bình luận (0)
Cho A = 1 + 2 + 2 2 + 2 3 + . . . + 2 50 . Chứng tỏ rằng: A + 1 là một lũy thừa của 2.
Bài 6: ( 1 điểm)
Cho A = 4 + 22 + 23 + ...+ 2300. Chứng tỏ rằng A là một lũy thừa cơ số 2.
Bài 6: ( 1 điểm)
Cho A = 4 + 22 + 23 + ...+ 2300. Chứng tỏ rằng A là một lũy thừa cơ số 2.
Lời giải:
$(2300-22):1+1=2279$
Tổng $A$ là:
$4+\frac{(2300+22).2279}{2}=2645923$. Số này lẻ nên không thể là lũy thừa cơ số 2.
Đúng 0
Bình luận (0)