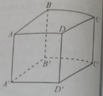
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:
A. 0 o
B. 45 o
C. 60 o
D. 90 o
Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD – bằng góc ACD
Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D
⇒ A C D ^ = 45 0
Đáp án B
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C’D’. Xác định góc giữa hai đường thẳng MN và AP
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP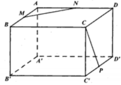
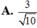
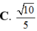
Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa hai đường thẳng AC và A’D.
A. 45 ∘
B. 30 ∘
C. 60 ∘
D. 90 ∘
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’C’ và BD bằng
A. 60 0
B. 30 0
C. 45 0
D. 90 0
Đáp án D.
Phương pháp giải: Dựng hình để xác định góc giữa hai đường thẳng chéo nhau: Góc giữa hai đường thẳng a và b là góc giữa a’ và b với a // a’.
Lời giải: Vì ABCD là hình vuông ⇒ A C ⊥ B D mà A C / / A ' C ' ⇒ A ' C ' ⊥ B D
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’C’ và BD bằng
A. 60 0
B. 30 0
C. 45 0
D. 90 0
Đáp án D
Phương pháp giải: Dựng hình để xác định góc giữa hai đường thẳng chéo nhau : Góc giữa hai đường thẳng a và b là góc giữa a’ và b với a // a’.
Lời giải: Vì ABCD là hình vuông ⇒ A C ⊥ B D mà A C / / A ' C ' ⇒ A ' C ' ⊥ B D .
Cho hình lập phương ABCD.A’B’C’D’ Góc giữa hai đường thẳng BA' và CD bằng:
A. 450
B.600
C. 300
D. 900
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng
A. 90⁰.
B. 30⁰.
C. 60⁰.
D. 45⁰.
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AB, BC. Tính góc của cặp đường thẳng MN và C’D’
A. 30º.
B. 45º.
C. 60º.
D. 90º
