chứng minh bất đẳng thức:ab2+bc2+ca2<=4

Những câu hỏi liên quan
Cho a,b,c > 0 và a+b+c=6
Chứng minh rằng : ab2 + bc2 + ca2 > (lớn hơn hoặc bằng) 24
Chú ý ab2 bc2 ca2 là ab bình phương bc bình phương và ca bình phương
Cho tam giác ABC . Kẻ BD vuông góc với AC( D∈AC) Chứng minh:3BD2+2AD2+CD2=AB2+BC2+CA2 thì tam giác ABC cân
Cho tam giác ABC có AB5, BC7,AC8
a) Từ đẳng thức overrightarrow{AC}-overrightarrow{AB}overrightarrow{BC} ,Chứng minh công thức 2overrightarrow{AB}.overrightarrow{AC} AB2+AC2-BC2
Tính overrightarrow{AB}.overrightarrow{AC} , rồi suay ra giá trị của góc A
b) Tính overrightarrow{CA}.overrightarrow{CB}
Đọc tiếp
Cho tam giác ABC có AB=5, BC=7,AC=8
a) Từ đẳng thức \(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\) ,Chứng minh công thức \(2\overrightarrow{AB}.\overrightarrow{AC}=\) AB2+AC2-BC2
Tính \(\overrightarrow{AB}.\overrightarrow{AC}\) , rồi suay ra giá trị của góc A
b) Tính \(\overrightarrow{CA}.\overrightarrow{CB}\)
a, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{BC}^2\)
\(\Leftrightarrow AC^2+AB^2-2\overrightarrow{AB}.\overrightarrow{AC}=BC^2\)
\(\Leftrightarrow2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}=\dfrac{5^2+8^2-7^2}{2}=20\)
b, \(2\overrightarrow{CA}.\overrightarrow{CB}=CA^2+CB^2-BC^2=CA^2\)
\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\dfrac{CA^2}{2}=\dfrac{8^2}{2}=32\)
Đúng 1
Bình luận (0)
Lời giải:
a)
\(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\)
\(\Rightarrow (\overrightarrow{AC}-\overrightarrow{AB})^2=\overrightarrow{BC}^2\Leftrightarrow AB^2+AC^2-2\overrightarrow{AC}.\overrightarrow{AB}=BC^2\)
\(\Leftrightarrow 2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\) (đpcm)
Ta có:
\(\overrightarrow{AB}.\overrightarrow{AC}=\frac{AB^2+AC^2-BC^2}{2}=\frac{5^2+8^2-7^2}{2}=20\)
\(\cos \angle A=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{20}{5.8}=\frac{1}{2}\)
\(\Rightarrow \angle A=60^0\)
b)
Tương tự phần a, \(\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-AB^2}{2}=\frac{8^2+7^2-5^2}{2}=44\)
Đúng 1
Bình luận (0)
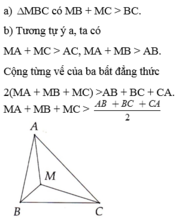
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.a) So sánh MB + MC với BCb) Chứng minh
M
A
+
M
B
+
M
C
A
B
+
B
C
+
C
A
2
Đọc tiếp
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2
Câu1
Từ một điểm tuỳ ý trên tam giác ABC, kẻ oa1, ob1, oc1 lần lượt vuông góc với bc, ca, ab. Chứng minh rằng ab 2/1+bc2/1+ca2/1=ac2/1+ba2/1+cb2/1
Câu 2
Cho tấm giác abc cân tại a, biết góc a=20 độ, bc=2cm. Trên cạnh ác lấy điểm d sao cho góc cbd=60 độ. Chứng minh ad=căn bậc hai của 2
Câu 1 : mình chỉ cách để cậu sao chéo link này nha .Đầu tiên bạn ấn chuột phải . Rồi ấn zô chữ in , sau đó cậu kéo xuống câu hỏi của cậu , xong cậu sao chép cái link ở dưới này nhá . Ok . Olm ko chụp ảnh đc .
https://scontent-sin6-2.xx.fbcdn.net/v/t1.15752-9/92245240_146128493508405_8939038888257650688_n.jpg?_nc_cat=105&_nc_sid=b96e70&_nc_ohc=X9iGs2rfBIcAX-BKDc4&_nc_ht=scontent-sin6-2.xx&oh=6f79129823e83db81e1c7ec56963fb48&oe=5EAE20C6
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh:
a) HA. HD = HB. HE = HC. HF
b) AH.AD + BH.BE + CH.CF = \(\dfrac{1}{2}\)(AB2 + BC2 + CA2)
c) H là giao điểm 3 đường phân giác của tam giác DEF.
Bất đẳng thức Cô - si là gì
Cách chứng minh bất đẳng thức Cô - si tối giản nhất ?
mk ko ghõ đc
Chắc do lỗi rồi
Câu trả lời của bạn đã được quản trị viện duyệt rồi nhé
HT
Xem thêm câu trả lời
Chứng minh bất đẳng thức Cô-si với n số không âm.
1) chứng minh bất đẳng thức Bu-nhi-a-cốp-ski với bộ n số.
Ai nhanh mình tick!^_^
chứng minh bất đẳng thức
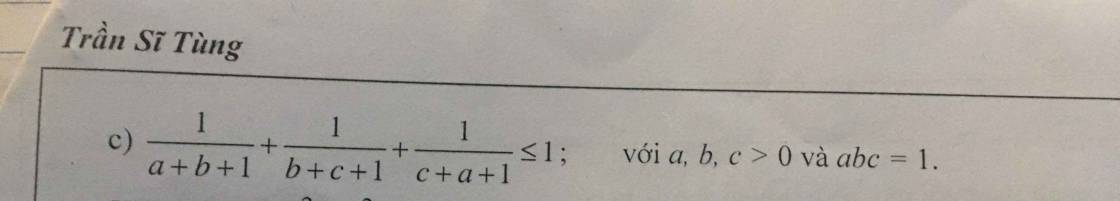
Sử dụng bất đẳng thức cô-si. Chứng minh bất đẳng thức \(\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge4\)
Lời giải:
Bổ sung điều kiện $a,b$ là các số dương. Áp dụng BĐT Cô-si ta có:
$a+b\geq 2\sqrt{ab}$
$\frac{1}{a}+\frac{1}{b}\geq 2\sqrt{\frac{1}{ab}}$
$\Rightarrow (a+b)(\frac{1}{a}+\frac{1}{b})\geq 2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4$
Ta có đpcm
Dấu "=" xảy ra khi $a=b$
Đúng 1
Bình luận (0)