Giá trị của x thuộc tập nào sau đây để thỏa mãn: \(\left|2x-4\right|=2x-4\)

Những câu hỏi liên quan
Giá trị của x thuộc tập nào sau đây để thỏa mãn: \(\left|2x-4\right|=2x-4\)
A. \([2;+\infty)\)
B. \(\left(-\infty;2\right)\)
C. \((-\infty;2]\)
D. \(\left(2;+\infty\right)\)
ĐK: \(x\ge2\)
PT \(\Leftrightarrow\left[{}\begin{matrix}2x-4=2x-4\\2x-4=4-2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\in R\\x=2\end{matrix}\right.\)
Kết hợp với điều kiện \(\Rightarrow x\ge2\)
Vậy \(x\in[2;+\infty)\)
Đúng 2
Bình luận (0)
Giá trị x thuộc tập nào sau đây để thỏa mãn: \(\left|x^2-4x+3\right|=x^2-4x+3\)
A. \(\left[1;3\right]\)
B. \((-\infty;1]\)
C. \((-\infty;1]\cup[3;+\infty)\)
D. \(\left(3;+\infty\right)\)
\(\left|x^2-4x+3\right|=x^2-4x+3\Leftrightarrow x^2-4x+3\ge0\)
\(\Rightarrow x\in(-\infty;1]\cup[3;+\infty)\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị m đểa) mx+6 2x+3m thỏa mãn m2b) mleft(2x-1right)ge2x+1 có tập nghiệm là [1;+infty)c) 2x-m 3left(x-1right) có tập nghiệm là left(4;+inftyright)d) mx+40 đúng với mọi left|xright| 8
Đọc tiếp
Tìm tất cả các giá trị m để
a) \(mx+6< 2x+3m\) thỏa mãn m<2
b) \(m\left(2x-1\right)\ge2x+1\) có tập nghiệm là \([1;+\infty)\)
c) \(2x-m< 3\left(x-1\right)\) có tập nghiệm là \(\left(4;+\infty\right)\)
d) \(mx+4>0\) đúng với mọi \(\left|x\right|< 8\)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
![]()
![]()
![]()
![]()
Đáp án A
Ta có, giả thiết
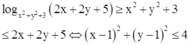
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và

Đúng 0
Bình luận (0)
Câu 1: Giá trị của x thỏa mãn
\(\left|x+2,37\right|+\left|y-5,3\right|=0\) là:.....
Câu 2: Giá trị của y thỏa mãn
\(-\left|2x+\frac{4}{7}\right|-\left|y-1,37\right|\) là:....
Câu 1: Giá trị của x thỏa mãn
|x+2,37|+|y−5,3|=0
Để GTBT bằng 0 thì |x+2,37| = 0 và |y−5,3| = 0
-> x = -2,37 , y = 5,3
Vậy x = -2,37
Câu 2: Giá trị của y thỏa mãn
−|2x+\(\frac{4}{7}\)|−|y−1,37| = 0
-> |2x+\(\frac{4}{7}\) = 0 -> x = \(-\frac{2}{7}\)
-> |y−1,37| = 0 -> y = 1,37
Vậy y = 1,37
Đúng 0
Bình luận (0)
Cho hệ pt : \(\left\{{}\begin{matrix}mx+3y=4\\2x-my=-3\end{matrix}\right.\)
a) Tìm m để HPT có vô số nghiệm
b) Với giá trị nào của m thì nghiệm của HPT thỏa mãn x<0 và y>0
cho các số thực dương x,y thỏa mãn \(\sqrt{y}\left(y+1\right)-6x-9=\left(2x+4\right)\sqrt{2x+3}-3y\). Tìm giá trị lớn nhất của biểu thức M = xy + 3y - 4\(x^2\) - 3
Đặt \(\left\{{}\begin{matrix}\sqrt{2x+3}=a\ge0\\\sqrt{y}=b\ge0\end{matrix}\right.\)
\(\Rightarrow b\left(b^2+1\right)-3a^2=\left(a^2+1\right)a-3b^2\)
\(\Rightarrow a^3-b^3+3a^2-3b^2+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+\left(a-b\right)\left(3a+3b\right)+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+3a+3b+1\right)=0\)
\(\Leftrightarrow a=b\Rightarrow\sqrt{2x+3}=\sqrt{y}\)
\(\Rightarrow y=2x+3\)
\(\Rightarrow M=x\left(2x+3\right)+3\left(2x+3\right)-4x^2-3\) tới đây chắc chỉ cần bấm máy
Đúng 0
Bình luận (0)
1/ Viết tập hợp các giá trị nguyên của x để \(x^2+4x+7⋮x+4\).
2/ Cho dãy số 1 ; 4 ; 9 ; 16 ; 25 ; 36 ; 49 ; ... Tìm số hạng thứ 80 của dãy.
3/ Tìm số các giá trị nguyên của x thỏa mãn: \(\left|2x+1\right|+\left|3-4x\right|+\left|6x+5\right|=2014\).
4/ Vẽ n tia chung gốc. Trong hình vẽ có 36 góc. Tính n.
3/ bạn lập bảng xét dấu là sẽ thấy có 4 trường hợp:
TH1: x<(-5/6), khi đó: -(2x+1)+[-(3-4x)]+[-(6x+5)]=2014
-2x-1-3+4x-6x-5=2014
-4x-9=2014
x=-2023/4 ( TM x<-5/6)
TH2: -5/6<=x<=-1/2, khi đó: 2x+1+[-(3-4x)]+[-(6x+5)]=2014
2x+1-3+4x-6x-5=2014
0x-7=2014 ( ko có giá trị x TM pt)
TH3:-1/2<=x<=3/4, khi đó: 2x+1+(3-4x)+[-(6x+5)]=2014
2x+1+3-4x-6x-5=2014
-8x-1=2014
x=-2015/8 ( ko TM -1/2<=x<=3/4 )
TH4: x>3/4; khi đó: 2x+1+3-4x+6x+5=2014
4x+9=2014
x=2005/4( TM x>3/4)
thế là xong. cái nào TM thì lấy
ghi chú <= là nhỏ hơn hoặc bằng
Đúng 0
Bình luận (0)
Câu 1: Giá trị x... thì biểu thức Dfrac{-1}{5}left(frac{1}{4}-2xright)^2-left|8x-1right|+2016 đạt giá trị lớn nhất. Câu 2: Tập hợp giá trị x nguyên thỏa mãn left|2x-7right|+left|2x+1right|le8Câu 3: Giá trị lớn nhất của B3-sqrt{x^2-25}Câu 4: Số phần tử của tập hợp left{xin Zleft|x-2right|le9right}Câu 5: Giá trị nhỏ nhất của biểu thức D frac{-3}{x^2+1}-2Câu 6: Có bao nhiêu cặp số (x;y) thỏa mãn đẳng thức xyx+yCâu 7: Gọi A là tập hợp các số nguyên dương sao cho giá trị của biểu thức: frac{2sqrt{x}+...
Đọc tiếp
Câu 1: Giá trị x=... thì biểu thức \(D=\frac{-1}{5}\left(\frac{1}{4}-2x\right)^2-\left|8x-1\right|+2016\) đạt giá trị lớn nhất.
Câu 2: Tập hợp giá trị x nguyên thỏa mãn \(\left|2x-7\right|+\left|2x+1\right|\le8\)
Câu 3: Giá trị lớn nhất của \(B=3-\sqrt{x^2-25}\)
Câu 4: Số phần tử của tập hợp \(\left\{x\in Z\left|x-2\right|\le9\right\}\)
Câu 5: Giá trị nhỏ nhất của biểu thức D= \(\frac{-3}{x^2+1}-2\)
Câu 6: Có bao nhiêu cặp số (x;y) thỏa mãn đẳng thức xy=x+y
Câu 7: Gọi A là tập hợp các số nguyên dương sao cho giá trị của biểu thức: \(\frac{2\sqrt{x}+3}{\sqrt{x}-1}\) là nguyên. Số phần tử của tập hợp A là...
Câu 8: Cho x;y là các số thỏa mãn \(\left(x+6\right)^2+\left|y-7\right|=0\) khi đó x+y=...
Câu 9: Phân số dương tối giản có mẫu khác 1, biết rằng tổng của tử và mẫu số bằng 18, nó có thể viết dưới dạng số thập phân hữu hạn. Có... phân số thỏa mãn















