Cho tam giác ABC cân tại A có góc A = 36 độ. vẽ phân giác BD. SO sánh DA và BD

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. góc A =36 độ. Vẽ phân giác BD. So sánh DA với DB
Xét ∆ABC ta có :
A + ABC + C = 180°
Mà ∆ABC cân tại A
=> ABC = C
=> ABC = C = \(\frac{180°-30°}{2}\)= 75°
Mà BD là phân giác ABC
=> ABD = CBD = \(\frac{75°}{2}\)=37,5°
Xét ∆ ABD ta có :
A + ADB + ABD = 180°
=> ADB = 180° - 30° - 37,5° = 112,5°
=> A < ABD < ADB
=> BD < AD< AB ( bất đẳng thức ∆)
=> BD< AD
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, góc A =36 độ. Vẽ phân giác BD. So sánh DA với DB. giúp tớ với ạ 😭😭😭😭
Từ đề bài ta suy ra ^ABD = 36o (Dễ dàng chứng minh). Từ đây suy ra tam giác ADB cân tại D. Do đó AD = DB.
Sai thì thôi!
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A = 36°. Vẽ phân giác BD. So sánh AD và BD?
Cho tam giác ABC cân tại A . Có góc A =36°
a, Tính góc B và C
b , Vẽ phân giâc BD chứng tỏ ABD cân
c, So sánh BD và BC
Giúp mk với cần gấp
Vì tam giác ABC cân tại A => B = C = (180 độ - 36 độ) : 2 = 72 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A và góc A=36 độ,vẽ phân giác B.So sánh DA với DB.
Cho tam giác abc cân tại A, có góc A = 36 độ. Vẽ tia phân giác BE của góc B( E thuộc AC). So sánh BE với AE và BC
Cho tam/g ABC có độ dài 3 cạnh: AB=7,2cm; BC=12cm;AC=9.6cm
a) C/m tam giác ABC là tam giác vuông
b) Vẽ đường AH vuôg góc vs BC tại H. So sánh BH và CH
c) Lấy D trên đoạn HC sao cho H là trug điểm của BD. C/m tam giác ABD cân
d) Vẽ CE vuông góc vs DA tại E. C/m CB là tia phân giác góc ACE
~~~~
Gíup mk vs ak
tu ve hinh :
tamgiac ABC co :
AB = 7,2 => AB2 = 7,22 = 51,84
BC = 12 => BC2 = 122 = 144
AC = 9,6 => AC2 = 9,62 = 92,16
=> AB2 + AC2 = 51,84 + 92,16 = 144 = BC2
=> tamgiac ABC vuong tai A (dinh ly Py-ta-go dao)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có AB > AC, tia phân giác của góc BAC cắt BC tại D. So sánh CD và BD.
2. Cho tam giác ABC cân tại A. Trên cạnh đáy BC lấy các điểm D, E sao cho BD = DE = EC. So sánh góc BAD và góc DAE.
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông góc tại A, phân giác BD. So sánh các độ dài BC và BD.
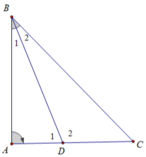
Cách 1. Xét tam giác ABD có ∠D2 là góc ngoài tam giác tại đỉnh D nên:
∠D2 = ∠B1 + ∠A
Suy ra: ∠D2 > ∠A (góc ngoài của ΔABD)
mà ∠A = 90o nên ∠D2 > 90o.
ΔBDC có ∠D2 > 90o nên ∠D2 > ∠C , do đó BC > BD.
Cách 2. Xét các đường xiên BD, BC.
Đoạn thẳng AD; AC lần lượt là hình chiếu của BD; BC trên đường thẳng AC.
Hình chiếu AC > AD nên đường xiên BC > BD. ( quan hệ đường xiên và hình chiếu của chúng ).
Đúng 0
Bình luận (0)
















