Cho hình vuông ABCD. Gọi O là giao của 2 đường chéo AC và BD. Kẻ đường thẳng d đi qua O. Kẻ \(AM\perp d\), \(BN\perp d\), \(CP\perp d\), \(DQ\perp d\)
CMR: \(AM^2+BN^2+CP^2+DQ^2\) không đổi không phụ thuộc vào vị trí của đường thẳng d
Những câu hỏi liên quan
cho hình vuông ABCD CÓ CẠNH BẰNG a , GỌI O LÀ GIAO ĐIỂM CỦA 2 ĐƯỜNG CHÉO. QUA O VẼ ĐƯỜNG THẲNG D . GỌI M,N,P,Q LÀ HÌNH CHIẾU CỦA A,B,C,D TRÊN ĐƯỜNG THẲNG D . TÍNH : AM^2 + BN^2 + CP^2 + DQ^2 THEO a
Bài 1: cho ΔMAB. Vẽ đường tròn tâm O , đường kính AB cắt MA tại C, cắt MB tại D. Kẻ AP ⊥ CD, PQ⊥CD. Gọi AD giao với BC tại H. Chứng minh:
a) CP=DQ
b) PD. DQ=PA. BQ
c) QC. CP=PD. QD
d) MA⊥AB
Bài 1: cho ΔMAB. Vẽ đường tròn tâm O , đường kính AB cắt MA tại C, cắt MB tại D. Kẻ AP ⊥ CD, PQ⊥CD. Gọi AD giao với BC tại H. Chứng minh:
a) CP=DQ
b) PD. DQ=PA. BQ
c) QC. CP=PD. QD
d) MA⊥AB
https://i.imgur.com/qLzMGGB.jpg
Cho O là tâm đối xứng của hình vuông ABCD, đường thẳng d qua O,M,N,P,Q lần lượt là hình chiếu của A,B,C,D trên d. Cạnh hình vuông là a.
Tính AM2+BN2+CP2+DQ2 theo a.
GIÚP MÌNH NHÉ
Cho hình bình hành ABCD, trên các cạnh AB, BC, CD, DA theo thứ tự lấy các điển M,N,P,Q sao cho AM=CP,BN=DQ.
a) CM:AMCP là hbh
b)Gọi O là giao điểm 2 đg chéo AC và BD, CM o là trung điểm MP
c)CM:MNPQ là hbh
d)CM: AC,BD,MP,NQ đồng quy tại 1 điểm
cho tam giác ABC cân , \(\widehat{A}=90^o\). qua A kẻ đường thẳng d tùy ý . Từ B và C kẻ \(BH\perp d,CK\perp d\). Chứng minh :\(BH^2+CK^2\)không phụ thuộc vào vị trí của đường thẳng d
Đề bài không đúng.
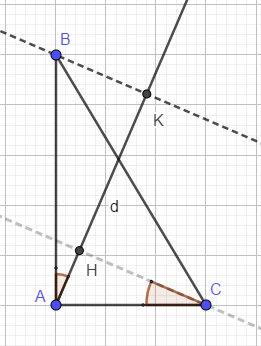
Đặt \(\alpha=\widehat{HCA};AB=c;AC=b\) thì \(\widehat{BAH=\alpha}\) và \(KB=c\sin\alpha;HC=b\cos\alpha\) từ đó
\(KB^2+HC^2=c^2\sin^2\alpha+b^2\cos^2\alpha\)
Nếu \(\alpha=45^0\)thì \(KB^2+HC^2=c^2\sin^245^0+b^2\cos^245^0=\frac{1}{2}\left(c^2+b^2\right)\).
Nếu \(\alpha=30^0\) thì \(KB^2+HC^2=c^2\sin^230^0+b^2\cos^230^0=\frac{1}{4}\left(c^2+3b^2\right)\).
Nếu \(\alpha=60^0\) thì \(KB^2+HC^2=c^2\sin^260^0+b^2\cos^260^0=\frac{1}{4}\left(3c^2+b^2\right)\).
Như vậy tổng \(KB^2+HC^2\) thay đổi khi đường thẳng d quay quanh A.
Đúng 0
Bình luận (0)
cho hình vuông ABCD . E là một điểm tùy ý trên đường chéo BD . Kẻ EM \(\perp\)AB, EN \(\perp\)AD.
a, cmr DM\(\perp\)CN
b, gọi I là giao điểm của BN và DM . CMR c, e,i thẳng hàng
Cho (O;R) và điểm I cố định nằm trong đường tròn (OIdR) , AC và BD là 2 dây cung vuông góc với nhau tại Ia, CMR: AB^2+CD^2AD^2+BC^24R^2b, Tính tổng bình phương 4 cạnh và tính tổng bình phương 2 đường chéo của tứ giác ABCD theo R và dc, Gọi M , N là trung điểm AB và CD . CMR: IMperp CDvà INperp ABd, CMR: Tứ giác OMIN là hình bình hànhe, CMR: Khi 2 dây cung AC và BD thay đổi và vuông góc với nhau tại I thì MN luôn đi qua 1 điểm cố định
Đọc tiếp
Cho (O;R) và điểm I cố định nằm trong đường tròn (OI=d<R) , AC và BD là 2 dây cung vuông góc với nhau tại I
a, CMR: \(AB^2+CD^2=AD^2+BC^2=4R^2\)
b, Tính tổng bình phương 4 cạnh và tính tổng bình phương 2 đường chéo của tứ giác ABCD theo R và d
c, Gọi M , N là trung điểm AB và CD . CMR: \(IM\perp CD\)và \(IN\perp AB\)
d, CMR: Tứ giác OMIN là hình bình hành
e, CMR: Khi 2 dây cung AC và BD thay đổi và vuông góc với nhau tại I thì MN luôn đi qua 1 điểm cố định
a) Kẻ đường kính DP của (O), ta có: BD vuông góc BP. Mà BD vuông góc AC nên BP // AC
=> (AP = (BC => (AB = (CP => AB = CP => AB2 + CD2 = CP2 + CD2 = DP2 = 4R2 (ĐL Pytagore)
Tương tự: AD2 + BC2 = 4R2 => ĐPCM.
b) Ta có: AB2 + BC2 + CD2 + DA2 = 4R2 + 4R2 = 8R2
Ta lại có: AC2 + BD2 = IA2 + IB2 + IC2 + ID2 + 2.IB.ID + 2.IA.IC = AB2 + CD2 + 4.IE.IF
= 4R2 + 4(R+d)(R-d) = 4R2 + 4R2 - 4d2 = 8R2 - 4d2
c) Gọi tia NI cắt AB tại H. Dễ thấy: ^BIH = ^NID = ^NDI = ^IAB = 900 - ^IBA => IN vuông góc AB.
C/m tương tự, ta có: IM vuông góc CD => ĐPCM.
d) Đường tròn (O): Dây AB, M trung điểm AB => OM vuông góc AB. Mà AB vuông góc IN => OM // IN
Tương tự ON // IM. Do đó: Tứ giác OMIN là hình bình hành (đpcm).
e) Vì tứ giác OMIN là hình bình hành nên MN đi qua trung điểm OI. Mà OI cố định NÊN trung điểm của OI cũng cố định nên ta có đpcm.
Đúng 0
Bình luận (0)
Chậc -_- bài này mình làm được lâu rồi bạn à :V Nhưng cũng cảm ơn , tớ nhờ cậu bài khác mà :(
Đúng 0
Bình luận (0)
11 tháng 11 2021 lúc 10:03
Cho hình vuông ABCD độ dài cạnh a có tâm O. Điểm M là 1 điểm di chuyển trên BC(M≠B,M≠C). Gọi N là giao điểm của tia AM và đường thẳng CD. G là giao của DM và BN.
a) CMR: \(\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\) không đổi
b) CM: \(CG\perp AN\)
c) Gọi H là giao của OM và BN. Tìm vị trí của M để \(S_{HAD}\) lớn nhất