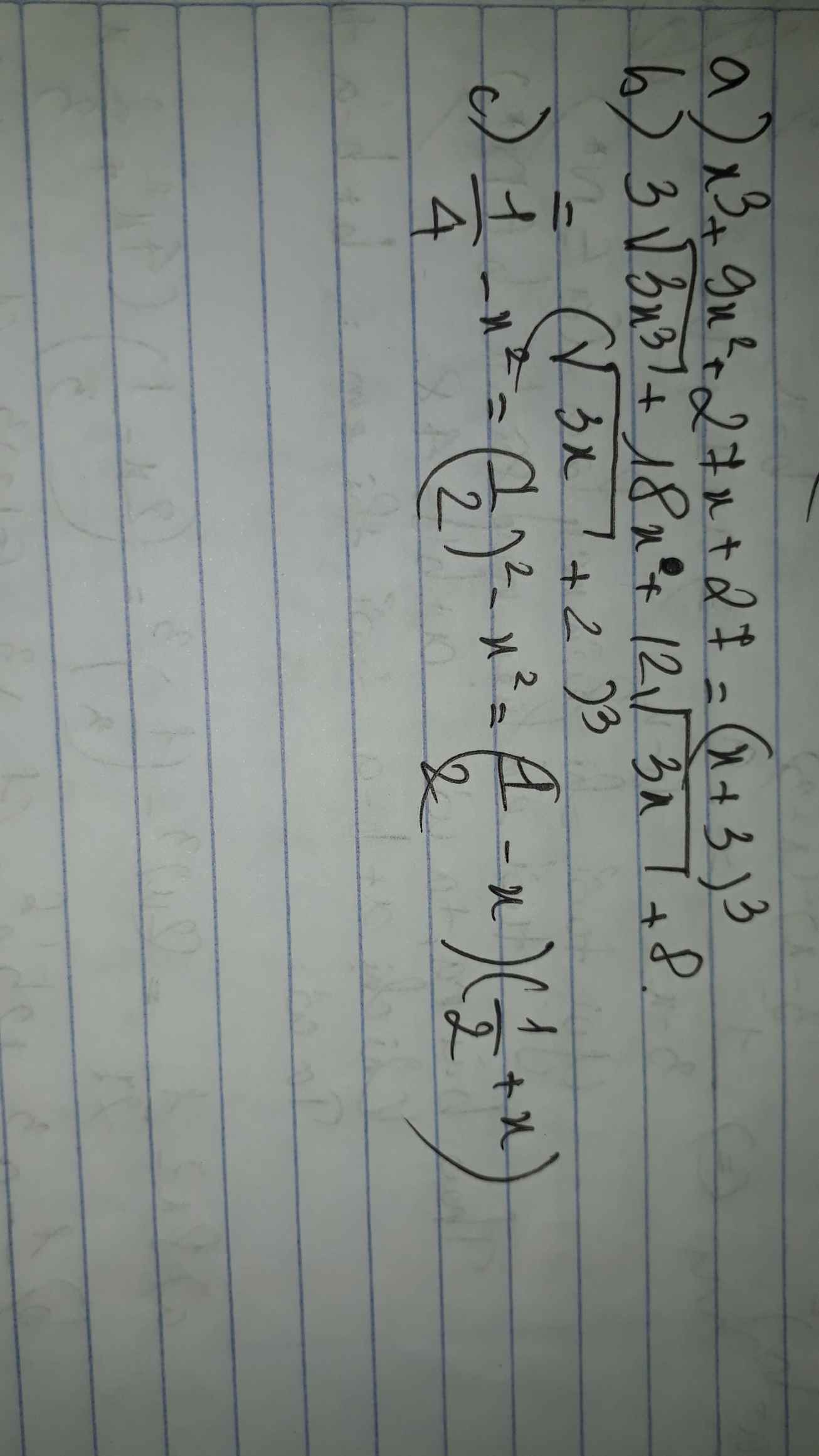\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)

#)Giải :

\(x^3-2x-4\)

\(=x^3+2x^2-2x^2+2x-4x-4\)

\(=x^3+2x^2+2x-2x^2-4x-4\)

\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)

\(=\left(x-2\right)\left(x^2+2x+2\right)\)

\(x^4+2x^3+5x^2+4x-12\)

\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)

\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)

\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)

\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)

Câu 1.

Đoán được nghiệm là 2.Ta giải như sau:

\(x^3-2x-4\)

\(=x^3-2x^2+2x^2-4x+2x-4\)

\(=x^2\left(x-2\right)+2x\left(x-2\right)+2\left(x-2\right)\)

\(=\left(x-2\right)\left(x^2+2x+2\right)\)

cảm ơn nha!

a) ( x + 1 )( x + 2 )( x + 3 )( x + 4 ) - 15

= [ ( x + 1 )( x + 4 ) ][ ( x + 2 )( x + 3 ) ] - 15

= ( x² + 5x + 4 )( x² + 5x + 6 ) - 15 (*)

Đặt t = x² + 5x + 4 

(*) trở thành

t( t + 2 ) - 15

= t² + 2t - 15

= t² - 3t + 5t - 15

= t( t - 3 ) + 5( t - 3 )

= ( t - 3 )( t + 5 )

= ( x² + 5x + 4 - 3 )( x² + 5x + 4 + 5 )

= ( x² + 5x + 1 )( x² + 5x + 9 )

b) ( x + 2 )( x + 3 )²( x + 4 ) - 12

= [ ( x + 2 )( x + 4 ) ]( x + 3 )² - 12

= ( x² + 6x + 8 )( x² + 6x + 9 ) - 12 (*)

Đặt t = x² + 6x + 8

(*) trở thành

t( t + 1 ) - 12

= t² + t - 12

= t² - 3t + 4t - 12

= t( t - 3 ) + 4( t - 3 )

= ( t - 3 )( t + 4 )

= ( x² + 6x + 8 - 3 )( x² + 6x + 8 + 4 )

= ( x² + 6x + 5 )( x² + 6x + 12 )

= ( x² + x + 5x + 5 )( x² + 6x + 12 )

= [ x( x + 1 ) + 5( x + 1 ) ]( x² + 6x + 12 )

= ( x + 1 )( x + 5 )( x² + 6x + 12 )

a, Gọi\(A=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-15\)

                \(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-15\)

Đặt\(y=x^2+5x+4\)

\(\Rightarrow A=y\left(y+2\right)-15\)

        \(=y^2+2y-15\)

        \(=\left(x-3\right)\left(x+5\right)\)

Hay\(A=\left(x^2+5x+1\right)\left(x^2+5x+9\right)\)

Vậy...

b,Gọi\(B=\left(x+2\right)\left(x+3\right)^2\left(x+4\right)-12\)

           \(=\left(x^2+6x+8\right)\left(x^2+6x+9\right)-12\)

Đặt\(z=x^2+6x+8\)

\(\Rightarrow B=z\left(z+1\right)-12\)

        \(=z^2+z-12\)

        \(=\left(z-3\right)\left(z+4\right)\)

Hay\(B=\left(x^2+6x+5\right)\left(x^2+6x+12\right)\)

Vậy...

Linz

\(a,\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-15\)

\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)-15\)

\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-15\)(*)

Đặt \(t=x^2+5x+4\)

(*)\(=t\left(t+2\right)-15\)

\(=t^2+2t-15\)

\(=t^2-3t+5t-15\)

\(=t\left(t-3\right)+5\left(t-3\right)\)

\(=\left(t-3\right)\left(t+5\right)\)

\(=\left(x^2+5x+4-3\right)\left(x^2+5x+4+3\right)\)

\(=\left(x^2+5x+1\right)\left(x^2+5x+9\right)\)

\(b,\left(x+2\right)\left(x+3\right)^2\left(x+4\right)-12\)

\(=\left(x+2\right)\left(x+4\right)\left(x+3\right)^2-12\)

\(=\left(x^2+6x+8\right)\left(x^2+6x+9\right)-12\)(*)

Đặt \(t=x^2+6x+8\)

(*)\(=t\left(t+1\right)-12\)

\(=t^2+t-12\)

\(=t^2-3t+4t-12\)

\(=t\left(t-3\right)+4\left(t-3\right)\)

\(=\left(t+4\right)\left(t-3\right)\)

\(=\left(x^2+6x+12\right)\left(x^2+6x+5\right)\)

\(=\left(x^2+6x+12\right)\left(x^2+x+5x+5\right)\)

\(=\left(x^2+6x+12\right)\left[x\left(x+1\right)+5\left(x+1\right)\right]\)

\(=\left(x^2+6x+12\right)\left(x+5\right)\left(x+1\right)\)

\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

\(\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)-80=\left(x^2-5x+4\right)\left(x^2-5x+6\right)-80\)

Đặt \(x^2-5x+4=t\), ta có:

\(t\left(t+2\right)-80=t^2-2t+1-81=\left(t-1\right)^2-9^2=\left(t-1-9\right)\left(t-1+9\right)=\left(t-10\right)\left(t+8\right)\)

\(=\left(x^2-5x+4-10\right)\left(x^2-5x+4+8\right)=\left(x^2-5x-6\right)\left(x^2-5x+12\right)\)

\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)

Đặt x² + x + 1 = t, ta có:

t(t + 1) - 12

= t² + t + 1/4 - 49/4

= (t + 1/2)² - (7/2)²

= (t + 1/2 + 7/2)(t + 1/2 - 7/2)

= (t + 4)(t - 3)

nhân váo như bình thường sau đó bấm máy tính shift solve =? rồi chia hoocne 

Câu b đề sai nha bạn.

a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)

b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)

c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)

Ta có: \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)

\(=\left(x^2+x\right)^2+3\left(x^2+x\right)+2-12\)

\(=\left(x^2+x\right)^2+3\left(x^2+x\right)-10\)

\(=\left(x^2+x+5\right)\left(x^2+x-2\right)\)

\(=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)