Cho tam giác nhọn ABC, hai đường cao BD và CE, Sade = 3/4 Sabc. Tính Â

Những câu hỏi liên quan
Tam giác abc nhọn. Góc a = 60 độ . Đường cao ce và bd. Cm: Sade=1/4 Sabc
Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
Xét ΔAED và ΔACB có
góc AED=góc ACB
góc A chung
=>ΔAED đồng dạng với ΔACB
=>S AED/S ACB=(AE/AC)^2=(cos60)^2=1/4
=>S AED=1/4*S ACB
Đúng 0
Bình luận (0)
Cho tam giác ABC, hai đường cao BD và CE
a. Chứng minh: AE.AB=AD.ACb. Chứng minh: góc ADE=ABC; góc AED=ABCc. Biết Â=60 độ, SABC= 120 cm\(^2\).Tính SADE?hế lô chào mk các streamer
Cho tam giác ABC, hai đường cao BD và CEa. Chứng minh AE.AB AD.ACb. Chứng minh góc ADE ABC góc AED ABCc. Biết  60 độ, SABC 120 cm2.Tính SADE
Cho tam giác nhọn ABC, hai đường cao BD và CE. Chứng minh S A D E = S A B C . cos 2 A
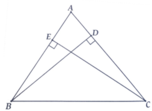
Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A
Đúng 0
Bình luận (0)
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạngvới ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, cac đường cao BD và CE cắt nhau tại H
a/CMR: \(\Delta AED\infty\Delta ACB\)(đã làm)
b/ DE cắt BC tại M. CMR MD.ME=MB.M(đã làm)
c/Biết A=600 và Sabc=12cm2. Tính Sade
c, Xét tam giác ADB vuông tại D có :
cosA = \(\frac{AD}{AB}=\frac{1}{2}\)
Lại có tam giác AED ~ tam giác ACB
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2\Rightarrow\frac{S_{ADE}}{12}=\frac{1}{4}\Rightarrow S_{ADE}=3\)cm2
:v bài này dùng cách lớp 8 đc k, mik chưa đc dùng cos
Bài 3 : Cho tam giác nhọn ABC, hai đường cao BF và CE.
a) Chứng minh tam giác AFB ~ tam giác AEC rồi suy ra AE.AB = AF.AC
b) Chứng minh góc AFE = góc ABC
c) Nếu Â=60 độ, SABC = 100cm2, tính SAFE ?
Bài 3 : Cho tam giác nhọn ABC, hai đường cao BF và CE.
a) Chứng minh tam giác AFB ~ tam giác AEC rồi suy ra AE.AB = AF.AC
b) Chứng minh góc AFE = góc ABC
c) Nếu Â=60 độ, SABC = 100cm2, tính SAFE ?
a: Xét ΔAFB vuông tại F và ΔAEC vuông tại E có
góc A chung
=>ΔAFB đồng dạng với ΔAEC
=>AF/AE=AB/AC
=>AF*AC=AB*AE
b: Xét ΔAFE và ΔABC có
AF/AB=AE/AC
góc A chung
=>ΔAFE đồng dạng với ΔABC
c: \(\dfrac{S_{AFE}}{S_{ABC}}=\left(\dfrac{AF}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{AFE}=25\left(cm^2\right)\)
Đúng 0
Bình luận (0)















