\(1)\sqrt{x^2+1}< 3.\\ \Leftrightarrow x^2+1< 9.\\ \Leftrightarrow x^2< 8.\\ \Leftrightarrow\left[{}\begin{matrix}x< 2\sqrt{2}.\\x>-2\sqrt{2}.\end{matrix}\right.\)

\(\Leftrightarrow-2\sqrt{2}< x< 2\sqrt{2}.\)

\(2)\dfrac{x^2-4x+3}{x^2-4}< 0.\)

Đặt \(f\left(x\right)=\dfrac{x^2-4x+3}{x^2-4}.\)

\(x^2-4=0.\Leftrightarrow\left[{}\begin{matrix}x=2.\\x=-2.\end{matrix}\right.\\ x^2-4x+3=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=1.\end{matrix}\right.\)

Bảng xét dấu:

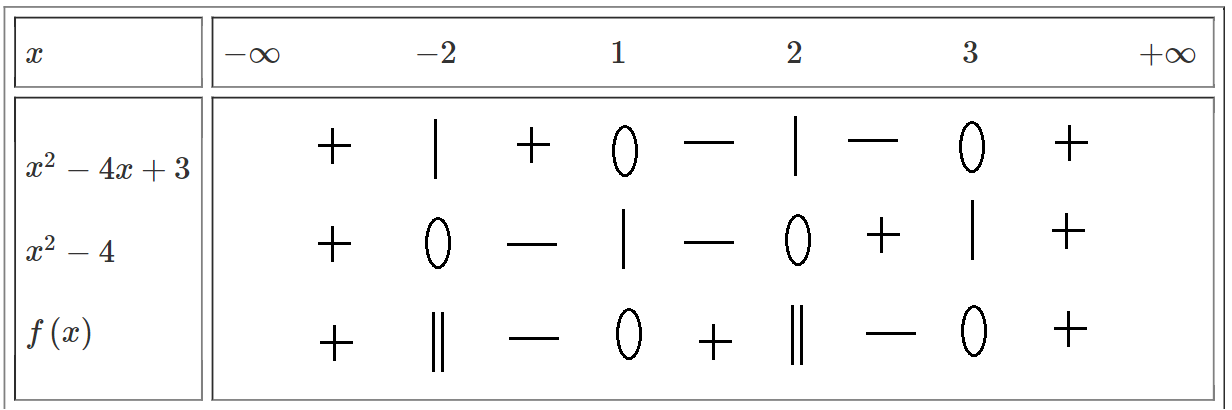
\(\Rightarrow f\left(x\right)< 0\Leftrightarrow x\in\left(-2;1\right)\cup\left(2;3\right).\)

Lời giải:

1.

$\sqrt{x^2+1}<3$

$\Leftrightarrow 0\leq x^2+1<9$

$\Leftrightarrow x^2+1<9$

$\Leftrightarrow x^2<8$

$\Leftrightarrow -2\sqrt{2}< x< 2\sqrt{2}$

2.

Xét 2 TH: 

TH1: \(\left\{\begin{matrix} x^2-4x+3<0\\ x^2-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)<0\\ (x-2)(x+2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 1< x< 3\\ x>2 \text{hoặc} x<-2\end{matrix}\right.\)

\(\Leftrightarrow 2< x<3\)

TH2: \(\left\{\begin{matrix} x^2-4x+3>0\\ x^2-4<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x-1)(x-3)>0\\ (x-2)(x+2)<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>3 \text{hoặc} x<1\\ -2< x< 2\end{matrix}\right.\)

\(\Leftrightarrow -2< x< 1\)

Kết hợp 2 TH suy ra tập nghiệm \(S=(2;3)\cup (-2;1)\)

\(x^2-2x=0\)

\(\Leftrightarrow x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

b.\(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)

\(ĐK:x\ne\pm2\)

\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)-5\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{12+\left(x^2-4\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Leftrightarrow\left(x+1\right)\left(x+2\right)-5\left(x-2\right)=12+\left(x^2-4\right)\)

\(\Leftrightarrow x^2+3x+2-5x+10=12+x^2-4\)

\(\Leftrightarrow-2x=-4\)

\(\Leftrightarrow x=2\left(ktm\right)\)

Vậy pt vô nghiệm

\(a,x^2-2x=0\)

\(\Leftrightarrow x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

\(b,\dfrac{x+1}{x-2}-\dfrac{5}{x-2}=\dfrac{12}{x^2-4}+1\) (ĐKXĐ : x ≠ 2 ; x ≠ -2)

\(\Rightarrow\left(x+1\right)\left(x+2\right)-5\left(x+2\right)=12+\left(x-2\right)\left(x+2\right)\)

\(\Leftrightarrow x^2+3x+2-5x-10=12+x^2+2x-2x+4\)

\(\Leftrightarrow2x=24\)

\(\Leftrightarrow x=12\left(N\right)\)

câu c chưa học :vv

a)

<=> x (x-2 ) = 0

<=> x =0 

x = 2

b)

đkxđ : x khác 2 , x khác -2

<=> \(\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{12}{x^2-4}+\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)

<=> \(\dfrac{x^2+3x+2}{....}-\dfrac{5x-10}{....}-\dfrac{12}{...}+\dfrac{x^2-4}{....}=0\)

<=> \(x^2+3x+2-5x+10-12+x^2-4=0\)

<=> \(2x^2-2x-4=0\)

<=> x =2 (ktm)

Vậy..

|x-9|=2x+5

Xét 3 TH

TH1: x>9 => x-9=2x+5 =>-9-5=x =>x=-14 (L)

TH2: x<9 => 9-x=2x+5 => 9-5=3x =>x=4/3(t/m)

TH3: x=9 =>0=23(L)

Vậy  x= 4/3

Ta có:\(\dfrac{1-2x}{4}-2\le\dfrac{1-5x}{8}+x\\ \)

\(\dfrac{2-4x-16}{8}\le\dfrac{1-5x+8x}{8}\)

\(-4x-14\le1+3x\\ \Leftrightarrow7x+15\ge0\\ \Leftrightarrow x\ge-\dfrac{15}{7}\)

Ta có:

\(\dfrac{2}{x-3}+\dfrac{3}{x+3}=\dfrac{3x+5}{x^2-9}\)

\(\dfrac{2\left(x+3\right)+3\left(x-3\right)}{x^2-9}=\dfrac{3x+5}{x^2-9}\)

\(5x-4=3x+5\Leftrightarrow2x=9\Leftrightarrow x=\dfrac{9}{2}\)

C

C

C

1: \(\Leftrightarrow\dfrac{3+2x-2}{x-1}>0\)

\(\Leftrightarrow\dfrac{2x+1}{x-1}>0\)

=>x>1 hoặc x<-1/2

2: \(\Leftrightarrow\dfrac{1-6x-2}{3x+1}< =0\)

\(\Leftrightarrow\dfrac{6x+1}{3x+1}>=0\)

=>x>1/3 hoặc x<=-1/6

\(\Leftrightarrow16-3\left(x+1\right)< 24+2\left(x-1\right)\)

=>16-3x-3<24+2x-2

=>-3x+13<2x+22

=>-5x<9

hay x>-9/5

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)    

Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)

Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)

          \(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)

Bảng xét dấu:

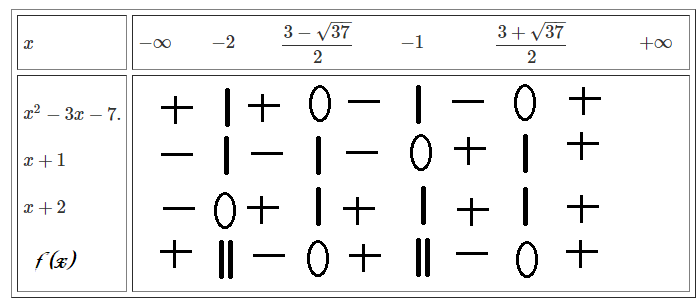
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)

\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)

Đặt \(f\left(x\right)=x^2-3x-7.\)

\(f\left(x\right)=x^2-3x-7.\)

\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)