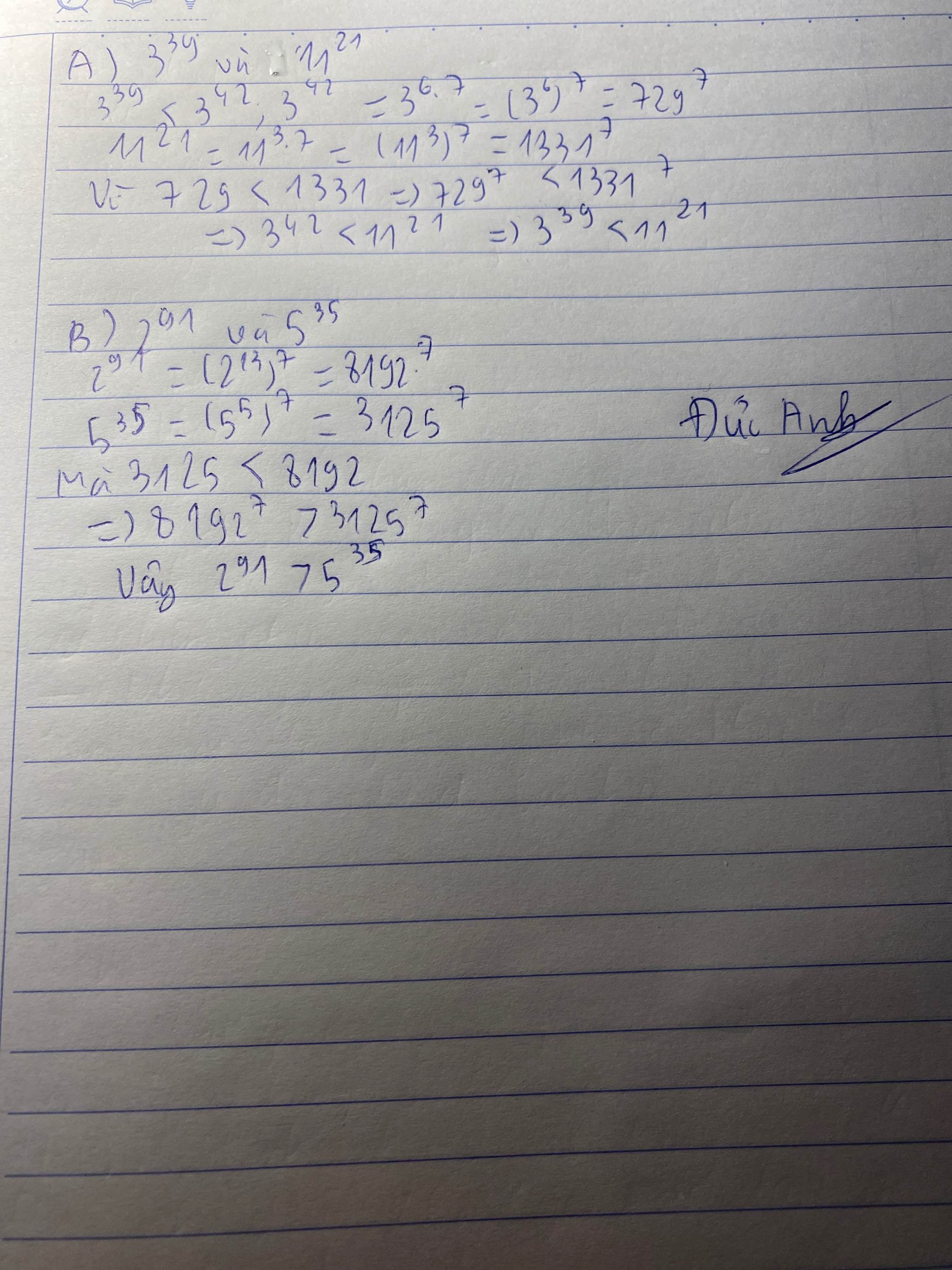2⁹¹ và 5³⁵

2⁹¹ = (2¹³)⁷ = 8192⁷

5³⁵ = (5⁵)⁷ = 3125⁷

Vì 8192⁷ > 3125⁷ => 2⁹¹ > 5³⁵

Vậy 2⁹¹ > 5³⁵

2⁹¹ <  5³⁵

2 mũ 21>5 mũ35

Ta có: 291 > 290 = (25)18 = 3218

535 < 536 = (52)18 = 2518.

Vì 32 > 25 nên 3218 > 2518, do đó ta có : 291 > 3218 > 2518 > 535.

Vậy 291 > 535.

`2^{91}=(2^{13})^{7}=8192^{7}`

`5^{35}=(5^{5})^{7}=3125^{7}`

Vì `8192^{7}>3125^{7}`

`->2^{91}>5^{35}`

\(2^{91}=\left(2^{13}\right)^7=8192^7\)

\(5^{35}=\left(5^5\right)^7=3125^7\)

Mà \(8192^7>3125^7\Rightarrow2^{91}>5^{35}\)

\(2^{91}=\left(2^{13}\right)^7\)

\(5^{35}=\left(5^5\right)^7\)

mà \(2^{13}>5^5\)

nên \(2^{91}>5^{35}\)

\(1,\\ a,2^x=16=2^4\Rightarrow x=4\\ b,3^{x+1}=9^x=3^{2x}\\ \Rightarrow x+1=2x\Rightarrow x=1\\ c,2^{3x+2}=4^{x+5}=2^{2\left(x+5\right)}\\ \Rightarrow3x+2=2x+10\Rightarrow x=8\\ d,3^{2x-1}=243=3^5\\ \Rightarrow2x-1=5\Rightarrow x=3\\ 2,\\ a,2^{225}=8^{75}< 9^{75}=3^{150}\\ b,2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\\ c,99^{20}=\left(99^2\right)^{10}< \left(99\cdot101\right)^{10}=9999^{10}\\ 3,\\ a,12^8\cdot9^{12}=2^{16}\cdot3^8\cdot3^{24}=2^{16}\cdot3^{32}=\left(2\cdot3^2\right)^{16}=18^{16}\\ b,75^{20}=\left(3\cdot5^2\right)^{20}=3^{20}\cdot5^{40}=\left(3^{20}\cdot5^{10}\right)\cdot5^{30}=\left(3^2\cdot5\right)^{10}\cdot5^{30}=45^{10}\cdot5^{30}\)

Bài 1:

a) \(\Rightarrow2^x=2^4\Rightarrow x=4\)

b) \(\Rightarrow3^{x+1}=3^{2x}\Rightarrow x+1=2x\Rightarrow x=1\)

c) \(\Rightarrow2^{3x+2}=2^{2x+10}\Rightarrow3x+2=2x+10\Rightarrow x=8\)

d) \(\Rightarrow3^{2x-1}=3^5\Rightarrow2x-1=5\Rightarrow x=3\)

Bài 2:

a) \(2^{225}=\left(2^3\right)^{75}=8^{75}< 9^{75}=\left(3^2\right)^{75}=3^{150}\)

b) \(2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\)

c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)

Bài 3:

a) \(12^8.9^{12}=\left(4.3\right)^8.9^{12}=4^8.3^8.9^{12}=2^{16}.9^4.9^{12}=2^{16}.9^{16}=\left(2.9\right)^{16}=18^{16}\)

b) \(75^{20}=\left(75^2\right)^{10}=5625^{10}=\left(45.125\right)^{10}=45^{10}.125^{10}=45^{10}.5^{30}\)

ai giúp mình nhanh đc ko

\(a,3^{39}=\left(3^3\right)^{13}=9^{13}< 11^{13}< 11^{21}\\ b,2^{91}=\left(2^{13}\right)^7=8192^7< 3125^7=\left(5^5\right)^7=5^{35}\)

Đây bạn nhé! Chữ hơi xấu, thông cảm

Ta có : \(\dfrac{-23}{91}>\dfrac{-131}{91}\\ \dfrac{-131}{91}>\dfrac{-131}{535}\\ nên\dfrac{-131}{535}>\dfrac{-23}{91}\)

\(a=\left[\left(-\dfrac{1}{2}\right)^5\right]^{107}=\left(-\dfrac{1}{32}\right)^{107}\)

\(b=\left[\left(-\dfrac{1}{3}\right)^3\right]^{107}=\left(-\dfrac{1}{27}\right)^{107}\)

mà -1/32>-1/27

nên a>b

a>b

Hôm qua lúc 15:07

So sánh :

a) 10¹⁰ và 48.50¹⁰

b) 22³³ và 33²²

d) 2⁹¹ và 5³⁵

a, 1010 < 48.5010

b, 2233 < 3322

c, 291 < 535