Cho tam giác CUP vuông tại C, CK là đường cao kẻ từ C Tìm một phép đồng dạng biến tam giác KUP thành tam giác CUP
đừng có ko là đk là bảo thiếu dữ liệu ,đúng 100% đấy
Cho tam giác CUP vuông tại C, CK là đường cao kẻ từ C Tìm một phép đồng dạng biến tam giác KUP thành tam giác CUP
o O O nguyễn tuán anh ê ,giải mk bài này mk tích cho bshn 1 tuần liền ok
Mik quên còn t/c đường phân giác nữa
Sorry nha
Nhưng chưa chắc đúng đâu sơ xài quá
Bài này ẩu kinh
Bạn biết phép đông dạng gồm :
Góc - Góc
Cạnh Cạnh cạnh
Cạnh canh góc
Ở đây thứ nhất thiếu dữ liệu
Thứ 2 thiếu hình
Thứ 3 chơi xỏ mik
ài này ẩu kinh
Bạn biết phép đông dạng gồm :
Góc - Góc
Cạnh Cạnh cạnh
Cạnh canh góc
Ở đây thứ nhất thiếu dữ liệu
Thứ 2 thiếu hình
Thứ 3 chơi xỏ mik
Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A, tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.
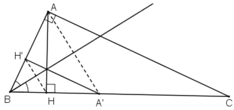
Gọi d là đường phân giác của góc B của ΔABC.
+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B
(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).
⇒ ΔH’BA’ = Đd(ΔHBA).
⇒ ΔH’BA’ = ΔHBA.
Mà ΔABC 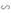 ΔHBA theo tỉ số
ΔHBA theo tỉ số 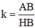
⇒ ΔABC 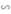 ΔH’BA’ theo tỉ số k
ΔH’BA’ theo tỉ số k
⇒ AB = k.H’B; BC = k.BA’.
Mà A ∈ tia BH’ ; C ∈ tia BA’
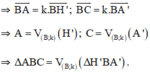
Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số 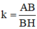 hợp với phép đối xứng trục d là phân giác của
hợp với phép đối xứng trục d là phân giác của 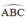
Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC ?
Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.
Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.
a) Gọi Bd là tia phân giác của \(\widehat{ABC}\).
Ta có: \(Đ_d\) biến tam giác AHB thành tam tam giác A'BH'.
Phép vị tự \(V_{\left(B;\dfrac{AH}{BC}\right)}\) biến tam giác A'BH thành tam giác CBA.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép \(Đ_d\) và \(V_{\left(B;\dfrac{AH}{BC}\right)}\) sẽ biến tam giác HBA thành tam giác ABC.
Cho tam giác ABC vuông tại C (AC<BC). Vẽ tia phân giác Ax của BAC cắt cạnh BC tại I. Vẽ BH vuông góc tại Ax tại H.
a) Chứng minh tam giác AIC đồng dạng tam giác ABH
b) Chứng minh HB 2 = HI.HA
c) Kẻ đường cao CK của tam giác ABC> Kẻ KD là đường phân giác của tam giác CKA. Chứng minh \(\dfrac{CD}{DA}=\dfrac{CB}{CA}\)
Xin hãy giúp mình với ạ! Mình xin cám ơn!
a: Xét ΔACI vuông tại C và ΔAHB vuông tại H có
góc CAI=góc HAB
=>ΔACI đồng dạng với ΔAHB
b: Xét ΔHBI và ΔHAB có
góc HBI=góc HAB
góc H chung
=>ΔHBI đồng dạng với ΔHAB
=>HB/HA=HI/HB
=>HB^2=HA*HI
c: CD/DA=CK/KA=CB/CA
a.
Xét hai tam giác AIC và ABH có:
\(\left\{{}\begin{matrix}\widehat{CAI}=\widehat{BAH}\left(\text{Ax là phân giác}\right)\\\widehat{ACI}=\widehat{AHB}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIC\sim\Delta ABH\left(g.g\right)\) (1)
b.
Xét hai tam giác AIC và BIH có:
\(\left\{{}\begin{matrix}\widehat{AIC}=\widehat{BIH}\left(\text{đối đỉnh}\right)\\\widehat{ACI}=\widehat{BHI}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AIC\sim\Delta BIH\left(g.g\right)\) (2)
(1);(2) \(\Rightarrow\Delta ABH\sim\Delta BIH\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{BH}{IH}\Rightarrow BH^2=HI.HA\)
c.
Áp dụng định lý phân giác trong tam giác ACK: \(\dfrac{CD}{DA}=\dfrac{CK}{AK}\) (3)
Xét hai tam giác ABC và ACK có:
\(\left\{{}\begin{matrix}\widehat{CAB}\text{ chung}\\\widehat{BCA}=\widehat{CKA}=90^0\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{BC}{CK}=\dfrac{AC}{AK}\Rightarrow\dfrac{BC}{AC}=\dfrac{CK}{AK}\) (4)
(3);(4) \(\Rightarrow\dfrac{CD}{DA}=\dfrac{BC}{AC}\)
Cho tam giác ABC vuông tại A có đường cao AH
a/ Chứng minh tam giác ABH đồng dạng tam giác CBA.
b/ Gọi M là trung điểm của BH. Kẻ CK vuông góc với AM tại K , CK cắt AH tại I. Chứng minh IA = IH
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: Xét ΔCAM có
CK,AH là đường cao
CK cắt AH tại I
=>I là trực tâm
=>MI vuông góc AC
=>MI//AB
Xét ΔHAB có
M là trung điểm của HB
MI//AB
=>I là trung điểm của AH
=>IA=IH
Cho tam giác ABC cân tại A . AH là đường cao. Từ H kẻ HM vuông góc AC tại M.
a) CM : tắm giác HMC đồng dạng với tam giác AHC
b) Gọi I là trung điểm HM. CM : tam giác HAI đồng dạng với tam giác CBM.
c) CM : AI vuông góc BM
Cho tam giác ABC vuông tại A có đường cao AH ( H thuộc BC)
a) Chứng minh : tam giác ABH đồng dạng tam giác CBA sau đó suy ra AB2= BH.BC
b) Chứng minh AH2=BH.CH
C) Gọi M là trung điểm của BH, kẻ CK vuông góc với AM tại K, CK cắt AH tại I. Chứng minh IA=IH
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
=>BA/BC=BH/BA
=>BA^2=BH*BC
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
c: Xét ΔCAM có
CK,AH là đường cao
CK cắt AH tại I
=>I là trực tâm
=>MI vuông góc AC
=>MI//AB
Xét ΔHAB có
M là trung điểm của HB
MI//AB
=>I là trung điểm của HA
Cho tam giác ABC vuông tại A, AH là đường cao.
a) Chứng minh: tam giác HBA đồng dạng với tam giác ABC
b) Chứng minh: tam giác HBA đồng dạng với tam giác HAC. Từ đó suy ra: AH.AH=BH.HC
c) Kẻ HD vuông góc với AB và HE vuông góc với AC. Chứng minh: tam giác AED đồng dạng với tam giác ABC
d) Nếu AB.AC=4AD.AE thì tam giác ABC là tam giác gì?
Mình đã giải xong câu a, b, c. Nhờ các bạn và quý thầy cô giải giúp câu d. Chỉ cần tóm tắt lời giải thôi cũng được ạ.
d) SADE = 1/2.AD.AE ; SABC = 1/2.AB.AC => SADE / SABC = AD.AE/AB.AC =1/4 (1)
Do tg ADE đồng dạng tg ABC => SADE / SABC = (DE/BC)2 = (AH/BC)2 (2)
Từ (1) và (2) => AH/BC = 1/2 hay AH = !/2 BC. Vậy AH là đường trung tuyến tg ABC, mà AH là đường cao => tg ABC cân tại A
cho tam giác abc vuông tại a , ab<ac , kẻ đường cao ah, phân giác bd. gọi i là giao điểm của ah và bd
a, cm tam giác abd đồng dạng tam giác hbi
b, cm ah2 = hb.hc
c,cm tam giác iad cân va da2 =dc.ih
d, ck vuông góc bd, kd vuông góc ac, q là trung điểm của bc. cm k,p,q thẳng hàng
a: Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔABD\(\sim\)ΔHBI
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
A) Ta cần chứng minh tam giác \(ABD\) đồng dạng tam giác \(HBI\). Để làm điều này, ta cần chứng minh rằng các góc của chúng là bằng nhau.
- Góc \(ABD\) và \(HBI\) là góc vuông, vì \(AB\) và \(HB\) là đường cao của tam giác \(ABC\).
- Góc \(ADB\) và \(HIB\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
Vậy, ta có thể kết luận tam giác \(ABD\) đồng dạng tam giác \(HBI\).
B) Để chứng minh \(AH^2 = HB \cdot HC\), ta sử dụng định lý đường cao và tính chất của đường cao trong tam giác vuông:
- \(AH\) là đường cao của tam giác \(ABC\), nên \(AH^2 = BH \cdot HC\).
Vậy, \(AH^2 = HB \cdot HC\).
C) Để chứng minh tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\), ta sử dụng tính chất của giao điểm của đường phân giác và đường cao:
- Góc \(IAD\) và \(IDA\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
- \(IH\) là đường cao của tam giác \(ABC\) nên \(DA^2 = DC \cdot IH\).
Vậy, ta chứng minh được tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\).
D) Để chứng minh \(K, P, Q\) thẳng hàng, ta có thể sử dụng tính chất của điểm trung điểm và đường phân giác:
- \(Q\) là trung điểm của \(BC\), nên \(Q\) nằm trên đường thẳng \(KP\).
- \(K\) là giao điểm của \(AH\) và \(BD\), và \(P\) là giao điểm của \(AH\) và \(CI\), nên \(K, P, Q\) thẳng hàng theo Định lý Menelaus trên tam giác \(ACI\) và đường thẳng \(KQ\).
Vậy, ta đã chứng minh được \(K, P, Q\) thẳng hàng.