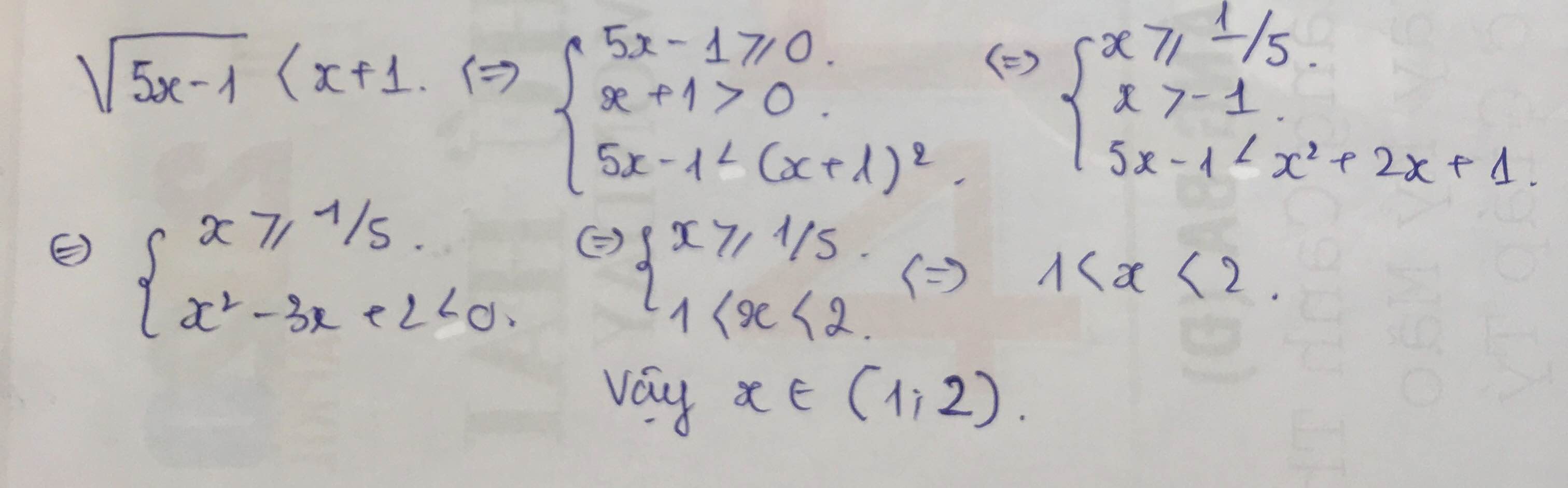2:

a: =>2x^2-4x-2=x^2-x-2

=>x^2-3x=0

=>x=0(loại) hoặc x=3

b: =>(x+1)(x+4)<0

=>-4<x<-1

d: =>x^2-2x-7=-x^2+6x-4

=>2x^2-8x-3=0

=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)

2x + 4 > 5x - 11

<=> 2x - 5x > -11 - 4

<=> -3x > -15

<=> -3x : ( -3 ) < -15 : ( -3 )

<=> x < 5

Vậy tập nghiệm của bất phương trình là x < 5 

2x²-5x+4<0

=>2( x²-\(\frac{5}{2}\).x +2)<0

=> 2(x²-\(\frac{5}{2}\).x+\(\frac{25}{16}\))+\(\frac{7}{8}\)<0

=>2(x-\(\frac{5}{4}\))²+\(\frac{7}{8}\)<0 (vô lí)

Vậy bất phương trình trên vô nghiệm

Có: \(\Delta=\left(-5\right)^2-4.2.4=-7< 0\)

mà 2 > 0

=> pt trên luôn luôn dương với mọi x thuộc R

mà đề cho: 2x² - 5x + 4 < 0 (vô lí)

                        Vậy x  thuộc rỗng

bạn học dental chưa z Ngô Hoài Thanh

a) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)

⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)

⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x

⇔ 10x ≥ 2 ⇔ x ≥ 1/5

Tập nghiệm: S = {x | x ≥ 1/5}

b) (x – 3)2 + 4(2 – x) > x(x + 7)

⇔ x2 – 6x + 9 + 8 – 4x > x2 + 7x

⇔ –17x > –17

⇔ x < -17/-17

⇔ x < 1

Tập nghiệm: S = {x | x < 1}.

Lời giải:

b/

\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)

c/

$2x^3+x+3>0$

$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$

$\Leftrightarrow (x+1)(2x^2-2x+3)>0$

$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$

$\Leftrightarrow x+1>0$

$\Leftrightarrow x>-1$

a) |3x| = x + 6 (1)

Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0

Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:

+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0

Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)

Do đó x = 3 là nghiệm của phương trình (1).

+ ) Phương trình -3x = x + 6 với điều kiện x < 0

Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)

Do đó x = -3/2 là nghiệm của phương trình (1).

Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}

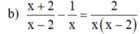
ĐKXĐ: x ≠ 0, x ≠ 2

Quy đồng mẫu hai vễ của phương trình, ta được:

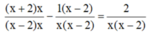
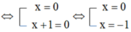
Vậy tập nghiệm của phương trình là S = {-1}

c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)

⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)

⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x

⇔ 10x ≥ 2 ⇔ x ≥ 1/5

Tập nghiệm: S = {x | x ≥ 1/5}

\(\dfrac{1-2x}{4}-2< \dfrac{1-5x}{8}\)

\(\Leftrightarrow\dfrac{2\left(1-2x\right)-16}{8}< \dfrac{1-5x}{8}\)

\(\Leftrightarrow2\left(1-2x\right)-16< 1-5x\)

\(\Leftrightarrow2-4x-16< 1-5x\)

\(\Leftrightarrow x< 15\)

Vậy \(S=\left\{x|x< 15\right\}\)