Cho hình thang ABCD có ABDC, AB \(\frac{1}{2}\)DC; AE = \(\frac{1}{3}\)AB. Diện tích hình tam giác EDC là 30cm2 .Tính diện thích hình thang ABCD.

Những câu hỏi liên quan
cho hình thang abcd có ab bằng 1 phần 2 dc, ae bằng 1 phần 3 ab, diện tích hình tam giác edc là 30 cm vuông. tính S hình thang abdc
Cho hình thang cân ABCD có AB//DC và AB<DC, đường chéo BD vuông góc với cạnh bên C.Về đường cao BH. a Chứng minh ABDC đồng dạng A HBC b Cho BC=15cm DC=25. Tính HC và HD • Tính diện tích hình thang ABCD.
a:Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có AB = 3cm, AD = 3cm, DC = 6cm. Trên DC lấy điểm M sao cho DM = \(\frac{1}{3}\)DC.
a) Diện tích hình thang ABCD là: ................
b) Diên tích hình tam giác BMC là:...............
Độ dài cạnh DM là : 6 nhân 1/3 = 2 (cm)
Diện tích hình thang ABCD là : ( 3 + 6) nhân 3 / 2 = 13,5 (cm2)
Diện tích hình tam giác BMC là : 6 nhân 3 / 2 = 9 ( cm2)
Đ/S : .....
Đúng 1
Bình luận (0)
Cho hình thang vuông ABCD có AB = 3cm, AD = 3cm, DC = 6cm. Trên DC lấy điểm M sao cho DM = \(\frac{1}{3}\) DC.
a) Diện tích hình thang ABCD là: ................
b) Diên tích hình tam giác BMC là:...............
Độ dài DM là : 6 x\(\frac{1}{3}\)= 2 ( cm )
Diện tích hình thang ABCD là : ( 3 + 6 ) x 3 : 2 = 13,5 ( \(cm^2\))
Diện tích tam giác BMC là : 6 x 3 : 2 = 4 (\(cm^2\) )
a) diện tích hình thang ABCD là : 13,5 \(cm^2\)
b) diện tích hình tam giác BMC là : 4\(cm^2\)
Đúng 0
Bình luận (0)
và mk cảm ơn mọi người rất nhiều
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD có AB = 1/2 DC ; AE = 1/3 AB; diện tích hình tam giác EDC là 30 cm2. Tính diện tích hình thang ABCD.
cho hình thang ABCD có AB =1/2 DC ; AE =1/3 AB ; diện tích hình tam giác EDC là 30 cm vuông . tính diện tích hình thang ABCD
Cho hình thang cân ABCD (AB//CD, AB < CD)ABCD(AB//CD,AB<CD). Kẻ hai đường cao AK, BMAK,BM của hình thang. Ta có thể kết luận:
+) DKDK >=< MCMC
+) DKDK = DC + AB(DC - AB) : 2DC - AB(DC + AB) : 2
cho hình thang ABCD vuông tại A và D . Có AB=AD=\(\frac{DC}{2}\). Tính các góc B và C của hình thang
Cho hình thang ABCD có
A
^
D
^
90
°
, DC BC 2.AB, DC 4cm. Tính góc ABC của hình thang. A.
110
°
B.
150
°
C.
120
°
D.
135
°
Đọc tiếp
Cho hình thang ABCD có A ^ = D ^ = 90 ° , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
A. 110 °
B. 150 °
C. 120 °
D. 135 °
Đáp án cần chọn là: C
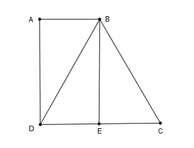
Từ B kẻ BE vuông góc với CD tại E.
Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.
Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.
Xét ΔBDE và ΔBCE có B E D ^ = B E C ^ = 90 ° ; DE = EC
BE cạnh chung nên ΔBED = ΔBEC (c – g – c)
Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.
Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên
E B C ^ = 1 2 D B C ^ = 1 2 × 60 ° = 30 °
Vì AD // BE mà B A D ^ = 90 ° nên A B E ^ = 180 ° - B A D ^ = 180 ° - 90 ° = 90 ° (hai góc trong cũng phía bù nhau)
Từ đó A B C ^ = A B E ^ + E B C ^ = 90 ° + 30 ° = 120 °
Vậy A B C ^ = 120 °
Đúng 0
Bình luận (0)















