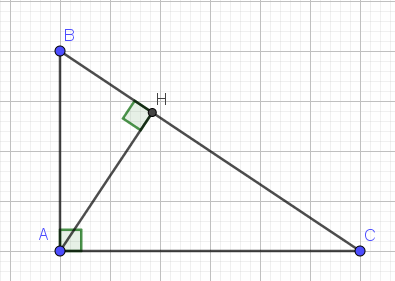
Bài 4: Cho tam giác ABC vuông tai A, đường cao AH ,biết AB = 15 cm, AH = 12cm a/ CM : AHB đồng dạngCHA b/ Tính các đoạn BH, CH , AC

Những câu hỏi liên quan
Bài 4: Cho tam giác ABC vuông tai A, đường cao AH ,biết AB = 15 cm, AH = 12cm a/ CM : AHB CHA b/ Tính các đoạn BH, CH , AC
a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó; ΔAHB∼ΔCHA
b: \(BH=\sqrt{AB^2-AH^2}=9\left(cm\right)\)
\(CH=\dfrac{AH^2}{BH}=16\left(cm\right)\)
AC=20cm
Đúng 0
Bình luận (0)
Câu 2. Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 15cm AH = 12cm
a) Chứng minh: tam giác AHB đồng dạng tam giác CHA b) Tính độ dài các đoạn BH, CH,ACLời giải:
a. Xét tam giác $AHB$ và $CHA$ có:
$\widehat{AHB}=\widehat{CHA}=90^0$
$\widehat{HAB}=\widehat{HCA}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle AHB\sim \triangle CHA$ (g.g)
b.
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Từ tam giác đồng dạng phần a suy ra $CH=\frac{AH^2}{BH}=\frac{12^2}{9}=16$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tai A, đường cao AH. Biết AB = 15 cm, AH = 12cm
a/ Chứng minh : ΔABC đồng dạng với ΔHBA
b/ Chứng minh ΔHBA đồng dạng ΔHAC
c/ Tính các đoạn BH, CH, AC.
d/ Chứng minh HA2 = HB.HC
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó:ΔHBA\(\sim\)ΔHAC
c: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(BC=\dfrac{AB^2}{BH}=\dfrac{15^2}{9}=25\left(cm\right)\)
\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
d: ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)
Đúng 5
Bình luận (0)
cho tam giác ABC vuông tại A , đường cao AH . biết AB=15cm , AH=12cm
a, CM tam giác AHB đồng dạng vs tam giác CHA
b, tinh BH,HC,AC
c, trên AC lấy E sao cho CE=5cm, trên BC lấy F sao cho CF=4cm . chứng minh tam giác CEF vuông
Cho tam giác ABC vuông tại A, có đường cao AH. Biết AB=15cm, AH=12cm.
a) Chứng minh tam giác AHB đồng dạng với tam giác CHA.
b) Tính độ dài cá đoạn thẳng BH,CH,AC.
c) Trên cạnh AC lấy điểm E sao cho CE=5cm,trên cạnh BC lấy điểm F sao cho CF=4cm. Chứng minh tam giác CEF vuông
Cho tam giác ABC vuông tại A ( AB>AC) đường cao AH a: CM tam giác ABC đồng dạng với tam giác HBA b: CM HA^2 = HB.HC c: cho AB =16 cm AC=12cm tính BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔACB vuông tại A có AH vuông góc BC
nên HA^2=HB*HC
c: \(CB=\sqrt{16^2+12^2}=20\left(cm\right)\)
BH=16^2/20=256/20=12,8cm
Đúng 1
Bình luận (1)
a) Xét △ABC và △HBA có:
Góc B chung
Góc BHA = góc BAC=90
⇒ △ABC ∼ △HBA ( g.g)
b)Xét △ABC có:
BC2=AB2+AC2
⇒BC=√(162+122)
⇔BC=20 (cm)
Ta có △ABC ∼ △HBA (g.g)
⇒AB/BC=AB/BH
⇔AB2 =BC.BH
⇔BH=AB2 /BC
⇒BH=162 /20=12,8 (cm)
Đúng 0
Bình luận (2)
Cho tam giác ABC vuông tại A ( AB>AC) đường cao AH a: CM tam giác ABC đồng dạng với tam giác HBA b: CM HA^2 = HB.HC c: cho AB =16 cm AC=12cm tính BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC vuông tại A có AH vuông góc CB
nên HA^2=HB*HC
c: \(BC=\sqrt{16^2+12^2}=20\left(cm\right)\)
HB=16^2/20=256/20=12,8cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B, đường cao BH. Chứng minh a. Tam giác ABC đồng dạng tam giác AHB và AB^2=AH.AC b. Tính AH biết, AB=6cm, AC=12cm
a) Xét ΔABC vuông tại B và ΔAHB vuông tại H có
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{AB}{AH}=\dfrac{AC}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AH\cdot AC\)
b) Ta có: \(AB^2=AH\cdot AC\)
\(\Leftrightarrow AH\cdot12=6^2=36\)
hay AH=3(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH.Cho biết: AB=15cm, AH=12cm
a) CM: tam giác ABH và tam giác CHA đồng dạng
b) Tính độ dài các đoạn thẳng BH,HC,AC ?
c) Trên cạnh AC lấy điểm E sao cho CE=5cm, trên cạnh BC lấy điểm F sao cho CF=4cm. Chứng minh tam giác CEF vuông ?
d) CM: CE.CA=CF.CB ?
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạngvới ΔHCA
b: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)
BC=15^2/9=25(cm)
\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
c: CE/CB=CF/CA
góc C chung
=>ΔCEF đồng dạng với ΔCBA
=>góc CFE=góc CAB=90 độ
=>ΔCEF vuông tại F
d: CE/CB=CF/CA
=>CE*CA=CF*CB
Đúng 0
Bình luận (0)