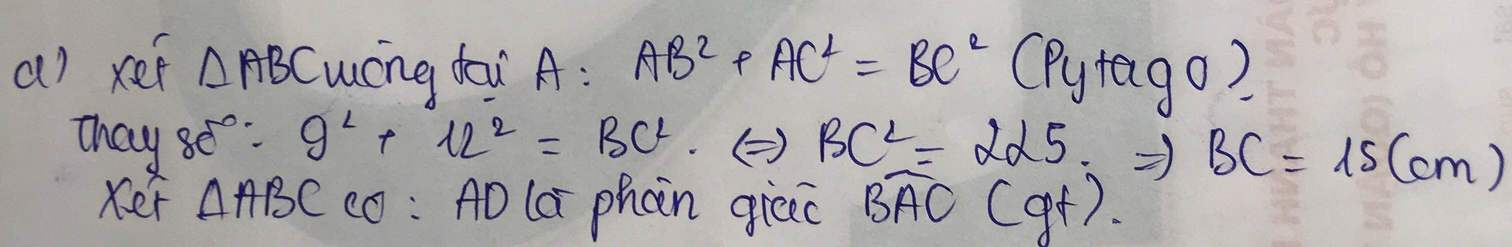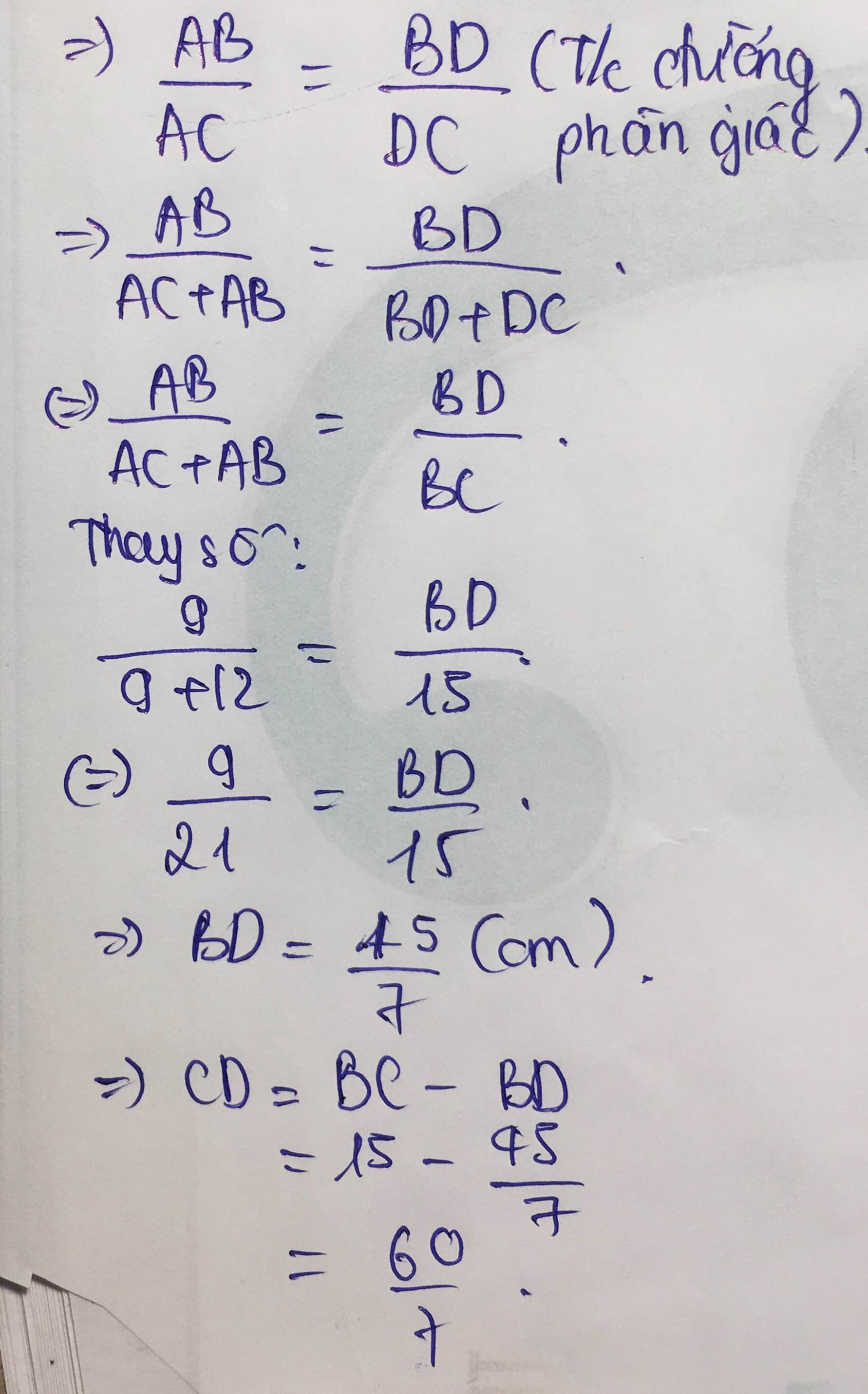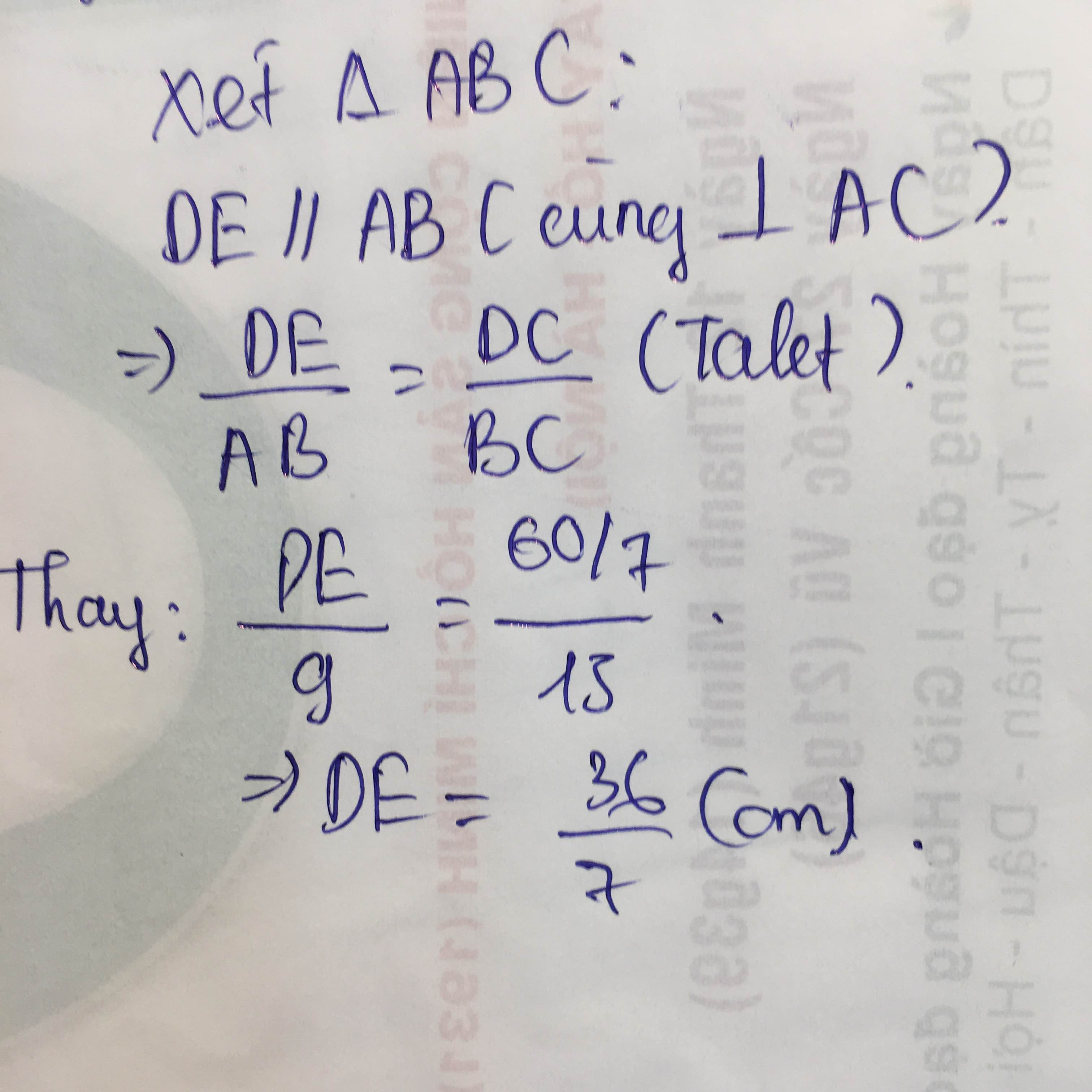Bài 1: Cho tam giác vuông ABC ( Â = 900 ) có AB = 9cm,AC = 12cm.Tia phân giác góc A cắt BC tại D .Từ D kẻ DE vuông góc với AC (E thuộc AC) .
a) Tính độ dài các đoạn thẳng BD,CD và DE.
b) Tính diện tích các tam giác ABD và ACD

Những câu hỏi liên quan
Bài 1: Cho tam giác vuông ABC ( Â = 900 ) có AB = 9cm,AC = 12cm.Tia phân giác góc A cắt BC tại D .Từ D kẻ DE vuông góc với AC (E thuộc AC) .
a) Tính độ dài các đoạn thẳng BD,CD và DE.
b) Tính diện tích các tam giác ABD và ACD
Bài 1. Cho tam giác vuông ABC ( Â = 90) có AB = 9cm,AC = 12cm.Tia phân giác góc A cắt BC tại D .Từ D kẻ DE vuông góc với AC (E thuộc AC) .
a) Tính độ dài các đoạn thẳng BD,CD và DE.
b) Tính diện tích các tam giác ABD và ACD.
Cho tam giác ABC vuông tại A có AB=9cm,AC=12cm.Tia phân giác của góc A cắt BC tại D,từ D kẻ DE vuông góc với AC tại E
a)Tính độ dài các đoạn thẳng BC,BD,CD và DE
b)Tính diện tích của các tam giác ABD và ACD
a) Ra có tam giác ABC vuông tại A ( gt )
\(\Rightarrow BC^2=AB^2+AC^2=9^2+12^2=81+144=225\left(cm\right)\)
\(\Rightarrow BC=15\left(cm\right)\)
Vì AD là tia phân giác của \(\widehat{BAC}\)( gt )
\(\Rightarrow\frac{DC}{DB}=\frac{AC}{AB}=\frac{12}{9}=\frac{4}{3}\Rightarrow\frac{DC+DB}{DB}=\frac{4+3}{3}=\frac{7}{3}\)\(\Rightarrow\frac{BC}{DB}=\frac{7}{3}\)
\(\Rightarrow DB=\frac{3}{7}.BC=\frac{3}{7}.15=\frac{45}{7}\left(cm\right)\)
\(\Rightarrow DC=15-\frac{45}{7}=\frac{60}{7}\left(cm\right)\)
Ta có DE // AB ( Vì AB và DE vuông góc với AC )
Áp dụng hệ quả định lý Ta lét ta có:
\(\Rightarrow\frac{DE}{AB}=\frac{CD}{CB}=\frac{60}{\frac{7}{15}}=\frac{4}{7}\)\(\Rightarrow DE=\frac{4}{7}.AB=\frac{4}{7}.9=\frac{36}{7}\left(cm\right)\)
b) Ta có: \(S_{ADC}=\frac{1}{2}.DE.AC=\frac{1}{2}.\frac{36}{7}.12=\frac{216}{7}\left(cm^2\right)\)
Ta có: \(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.9.12=54\left(cm^2\right)\)
\(\Rightarrow S_{ABD}=S_{ABC}-S_{ACD}=54-\frac{216}{7}=\frac{126}{7}\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC góc A bằng 90 độ có AB=9cm AC=12cm.Tia phân giác góc A cắt BC tại D.Từ D kẻ DE vuông góc với AC (E thuộc AC)
a) Tính độ dài đoạn thẳng BD,CD và DE
b) tính diện tích tam giác ABD và ACD
Bài 5 :Cho tam giác ABC vuông tại A có AB = 9cm, AC = 12cm. Tia phân giác góc A cắt BC tại D. Từ D kẻ DE vuông góc với AC (E thuộc AC)
a) Tính độ dài các đoạn thẳng BD, CD, DE
b) Tính diện tích tam giác ABD và ACD
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{9}=\dfrac{CD}{12}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{9}=\dfrac{CD}{12}=\dfrac{BD+CD}{9+12}=\dfrac{BC}{21}=\dfrac{15}{21}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{9}=\dfrac{5}{7}\\\dfrac{CD}{12}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{45}{7}cm\\CD=\dfrac{60}{7}cm\end{matrix}\right.\)
Vậy: \(BD=\dfrac{45}{7}cm;CD=\dfrac{60}{7}cm\)
Đúng 3
Bình luận (0)
cho tam giác ABC vuông tại A , có AB = 9cm , AC = 12cm . tia phân giác của góc A cắt BC tại D . từ d kẻ DE vuông góc với AC ( E thuộc AC)
a) tính độ dài của đoạn thẳng bc , bd , cd và de
b) tính diện tích của tam giác ABD và ACD
Cho tam giác ABC vuông tại A , có AB = 9cm , AC = 12cm . Tia phân giác của góc A cắt BC tại D . Từ D kẻ DE vuông góc với AC ( E thuộc AC ) a, chứng minh Δ ABC đồng dạng ΔEDC b, tính độ dài các đoạn thẳng BC , BD , CD
Cho tam giác ABC vuông tại A có AB = 9cm, AC = 12cm. Tia phân giác góc A cắt BC tại D. Từ D kẻ DE vuông góc với AC (E thuộc AC).
a,Tính độ dài các đoạn thẳng BD, BC, CD.
b,Chứng minh tam giác ABC đồng dạng với tam giác EDC.
c,Tính DE
d,Tính tỉ số SABD/SADC
Vẽ hình, viết giả thiết kết luận và giải giúp mik với :<
*Mọi người ơi, giúp mình bài này với*
Cho tam giác vuông ABC ( A=90 độ) có AB = 9cm, AC = 12cm. Tia phân giác của góc A cắt BC tại D. Từ D kẻ DE⊥AC (E ∈ AC).
a) Tính độ dài các đoạn thẳng BD, CE và DE
b) Tính diện tích các tam giác ABD và ACD