Cho 2 đường thẳng a và b cắt nhau tại O. Tính các góc O1,O2,O3,O4 nếu O1+O3=O2+O4.

Những câu hỏi liên quan
Cho hai đường thẳng ab và cd cắt nhau tại O, tạo thành các góc tại đỉnh O là góc O1,góc O2, góc O3, góc O4, biết góc O1- góc O2=40°. Tính các góc tại đỉnh O.
\(\widehat{O_1}=\widehat{O_3}=110^0;\widehat{O_2}=\widehat{O_4}=70^0\)
Đúng 0
Bình luận (0)
làm đc mình tick luôn nha
bài1 vẽ hai đường xx' và yy' cắt nhau trong các góc tạo thành có một góc bằng 60 độ.Tính các số đo góc còn lại
bài 2: Hai đường thẳng cắt nhau tại O tạo thành các góc như hình vẽ sau. tính số đo các góc O1,O2,O3,O4, biết:
a, O1+O3=180 độ
b, O1= 1/4 O2
C, O2-O1= 50 độ
d, O1+O3= 2/3 ( O2+O4)
bài1
Giả sử trong hình bên, hai đường thẳng xx’ và yy’ cắt nhau tại O, góc xOy bằng 60o
Ta có: ∠xOy = ∠x’Oy'(hai góc đối đỉnh)
Suy ra ∠x’Oy’=60o.
∠xOy + ∠x’Oy’= 180o (hai góc kề bù)
⇒ ∠x’Oy’ = 180o – ∠xOy = 180o – 60o = 120o
∠xOy’ = ∠x’Oy(hai góc đối đỉnh)
⇒∠x’Oy=120o
hai đường thẳng cắt nhau tạo thành 4 góc O1, O2, O3, O4. Tính các góc còn lại biết O2-O1=30
Ta có: ∠O1 + ∠O2 = 1800 (2 góc kề bù)
Mà ∠O2 − ∠O1 =300
⇒ 2.∠O2 = 1800 + 300 = 2100
⇒ ∠O2 = 2100:2 = 1050 ⇒ ∠O2 = ∠O4 = 1050 (đối đỉnh)
⇒ ∠O1 = 1800 −1050 = 750 ⇒ ∠O1 = ∠O3 = 750 (đối đỉnh)
Đúng 3
Bình luận (0)
Hai đường thẳng cắt nhau tạo thành 4 góc O1, O2, O3, O4. Tính các góc còn lại biết O2-O1=30
Giải:
Ta có: ∠O1 + ∠O2 = 1800 (2 góc kề bù)
Mà ∠O2 − ∠O1 =300
⇒ 2.∠O2 = 1800 + 300 = 2100
⇒ ∠O2 = 2100:2 = 1050 ⇒ ∠O2 =∠O4 = 1050 (đối đỉnh)
⇒ ∠O1 = 1800 −1050 = 750 ⇒ ∠O1 = ∠O3 = 750 (đối đỉnh)
Đúng 1
Bình luận (1)
Giải:
Ta có: ∠O1 + ∠O2 = 1800 (2 góc kề bù)
Mà ∠O2 − ∠O1 =300
⇒ 2.∠O2 = 1800 + 300 = 2100
⇒ ∠O2 = 2100:2 = 1050 ⇒ ∠O2 =∠O4 = 1050 (đối đỉnh)
⇒ ∠O1 = 1800 −1050 = 750 ⇒ ∠O1 = ∠O3 = 750 (đối đỉnh)
Đúng 0
Bình luận (0)
Hai đường thẳng cắt nhau tạo thành 4 góc :góc O1;O2;O3;O4. Tính các góc còn lại trong các trường hợp sau:
a) <O1+<O3=140o
b) <O1+<O2+<O3=240o
c) <O2-<O1=30o
d) <O2=2 < O1
e) <O1 =75o
Hai đường thawneg cắt nhau tạo thành 4 góc :góc O1;O2;O3;O4. Tính các góc còn lại trong các trường hợp sau:
a) Góc O1+O3=140 độ
b) O1+O2+O3=240 độ
c) O2-O1=30 độ
e) O2=2 góc O1
Cho hình vẽ. Tính
O
1
^
,
O
2
^
,
O
3
^
,
O
4
^
nếu biết:a)
O
1
^
1
2
O
2...
Đọc tiếp
Cho hình vẽ. Tính O 1 ^ , O 2 ^ , O 3 ^ , O 4 ^ nếu biết:
a) O 1 ^ = 1 2 O 2 ^
b) O 2 ^ − O 1 ^ = 40 0
c) O 1 ^ + O 3 ^ = 130 0
d) O 1 ^ + O 2 ^ + O 3 ^ = 250 0
e) O 1 ^ + O 3 ^ = 1 2 ( O 2 ^ + O 4 ^ )
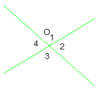
Cho hình vẽ. Tính O 1 ^ , O 2 ^ , O 3 ^ , O 4 ^ nếu biết:
a) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 1 ^ = 1 2 O 2 ^ nên
1 2 O 2 ^ + O 2 ^ = 180 0 ⇒ 3 2 O 2 ^ = 180 0 ⇒ O 2 ^ = 180 0 .2 3 = 120 0
O 1 ^ = 1 2 O 2 ^ ⇒ O 1 ^ = 1 2 .120 0 = 60 0
Vậy O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = O 4 ^ = 120 0
b) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 2 ^ − O 1 ^ = 40 0
⇒ 2 O 2 ^ = 220 0 ⇒ O 2 ^ = 110 0
O 2 ^ − O 1 ^ = 40 0 ⇒ 120 0 − O 1 ^ = 40 0 ⇒ O 1 ^ = 70 0
Vậy O 1 ^ = O 3 ^ = 70 0 ; O 2 ^ = O 4 ^ = 110 0
c) O 1 ^ + O 3 ^ = 130 0 Mà O 1 ^ = O 3 ^ ( Đối đỉnh) nên O 1 ^ = O 3 ^ = 130 0 : 2 = 65 0
O 2 ^ = O 4 ^ = 180 0 − 65 0 = 115 0 ( Hai góc kè bù)
d) O 1 ^ + O 2 ^ + O 3 ^ = 250 0
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) nên O 3 ^ = 250 0 − 180 0 = 70 0 .
Do đó O 1 ^ = O 3 ^ = 70 0 ( Đối đỉnh)
O 2 ^ = 180 0 − 70 0 = 110 0 . Suy ra O 4 ^ = O 2 ^ = 110 0 ( Đối đỉnh)
e) O 1 ^ + O 3 ^ = 1 2 ( O 2 ^ + O 4 ^ )
Mà O 1 ^ = O 3 ^ ( Đối đỉnh) , O 4 ^ = O 2 ^ ( Đối đỉnh)
Suy ra 2 O 1 ^ = 1 2 .2 O 2 ^ ⇒ 2 O 1 ^ = O 2 ^
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù). Suy ra O 1 ^ + 2 O 1 ^ = 180 0 ⇒ O 1 ^ = 60 0
O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = 2 O 1 ^ = 60 0 .2 = 120 0 ⇒ O 4 ^ = O 2 ^ = 120 0
Đúng 0
Bình luận (0)
Hai đường thẳng cắt nhau tạo thành 4 góc :góc O1;O2;O3;O4. Tính các góc còn lại trong các trường hợp sau:
a) <O1+<O3=140o
b) <O1+<O2+<O3=240o
c) <O2-<O1=30o
d) <O2=2 < O1
e) <O1 =75o
ai lam nhanh minh tich cho
Giải: a) Ta có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
mà \(\widehat{O_1}+\widehat{O_3}=140^0\)
=> \(\widehat{O_1}=\widehat{O_3}=70^0\)
Ta lại có: \(\widehat{O_1}+\widehat{O_2}=180^0\)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-70^0=110^0\)
=> \(\widehat{O_2}=\widehat{O_4}=110^0\) (đối đỉnh)
b) Ta có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=240^0\)
mà \(\widehat{O_1}+\widehat{O_2}=180^0\)(kề bù)
=> \(\widehat{O_3}=240^0-\left(\widehat{O_1}+\widehat{O_2}\right)=240^0-180^0=60^0\)
=> \(\widehat{O_3}=\widehat{O_1}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-60^0=120^0\)
=> \(\widehat{O_2}=\widehat{O_4}=120^0\) (đối đỉnh)
c) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
mà \(\widehat{O_2}-\widehat{O_1}=30^0\)
=> \(2.\widehat{O_2}=180^0+30^0=210^0\)
=> \(\widehat{O_2}=210^0:2=105^0\) => \(\widehat{O_2}=\widehat{O_4}=105^0\)(đối đỉnh)
=> \(\widehat{O_1}=180^0-105^0=75^0\) => \(\widehat{O_1}=\widehat{O_3}=75^0\) (đối đỉnh)
d) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_1}+2.\widehat{O_1}=180^0\)
=> \(3.\widehat{O_1}=180^0\)
=> \(\widehat{O_1}=180^0:3=60^0\) => \(\widehat{O_1}=\widehat{O_3}=60^0\) (đối đỉnh)
=> \(\widehat{O_2}=180^0-60^0=120^0\) => \(\widehat{O_2}=\widehat{O_4}=120^0\) (Đối đỉnh)
e) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-75^0=105^0\)
=> \(\widehat{O_2}=\widehat{O_4}=105^0\) (đối đỉnh)
Ta lại có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
Mà \(\widehat{O_1}=75^0\) => \(\widehat{O_3}=75^0\)
Đúng 0
Bình luận (0)
Hai đường thẳng LM và NP cắt nhau tại O. Biết rằng ^O2 - ^O3 = 12°.
Tìm số đo các góc sau:
^O4 = °
^O1 = °
\(\left\{{}\begin{matrix}\widehat{O_2}+\widehat{O_3}=180^0\left(kề.bù\right)\\\widehat{O_2}-\widehat{O_3}=12^0\left(kề.bù\right)\end{matrix}\right.\Rightarrow\widehat{O_2}=\left(180^0+12^0\right):2=96^0;\widehat{O_3}=84^0\)
\(\widehat{O_3}=\widehat{O_1}=84^0;\widehat{O_2}=\widehat{O_4}=96^0\left(các.cặp.góc.đối.đỉnh\right)\)
Đúng 6
Bình luận (0)
Hai đường thẳng LM và NP cắt nhau tại O. Biết rằng O1 O2 40°.Tìm số đo các góc sau O3 ° O4 °























