Giải phương trình chứa ẩn ở mẫu mà ra kết quả 0x=0 thì kết luận như thế nào
Với những dạng bài giải phương trình/bất phương trình mà có kết quả như thế này thì kết luận sao ạ?
\(0=0\) (luôn đúng)
\(-1>0\) (vô lí)
0=0 thì pt thoả mãn với mọi x
-1>0 pt vô nghiệm \(S=\varnothing\)
`1.` Với `0=0(` luôn đúng `)` `->` Kết luận: Vậy `S={x|x\inRR}`
`2.` Với `-1>0(` vô lý `)` `->` Kết luận: Vậy `S=∅`
Phương trình chứa ẩn ở mẫu thì phải có ĐKXĐ để mẫu khác 0, và phải khử mẫu và còn phải loại những giá trị không thỏa mãn ĐK
Phương trình không chứa ẩn ở mẫu thì chỉ cần giải phương trình như bình thường
cho mình hỏi , giải pt ra kết quả 0x= 1 số bất kì; x=0 thì kết luận sao vậy mọi người?
bạn cứ ghi là:
Vậy phương trình có tập nghiệm: S={0}
hoặc
Vậy phương trình có nghiệm: x = 0
bỏ cái x=0 đi
0x=1(vô lý)
xong kết luận là : vậy phương trình vô nghiệm
Khi nghiệm của một phương trình chứa ẩn x bằng 0 thì phương trình đó như thế nào ?
Mọi người chỉ mình ạ!
Bài 1: giải phương trình
\(\sqrt{5x^2}=2x-1\)
* Chỉ mình tại sao bài này nếu mà bình phương 2 vế lên có giải được ra kết quả đúng không ạ. Giair thích rõ và chi tiết giúp mình nhé
* Với nhưng dạng thế nào thì có thể bình phương ạ!
Bài 2: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
* Với bài này mình chưa tìm điều kiện luôn mà giải ra thành \(\sqrt{x+1}=1\) rồi tìm điều kiện \(x+1\ge0\) cũng được ạ các bạn.
* Nó có phụ thuộc vào dạng bài không ạ hay là chỉ có những bài mới được làm như vậy còn chỉ có những bài thì phải tìm điều kiện ngay từ đầu ạ ( và làm như vậy có bị mất trường hợp nào đi không) . giải thích tại sao
Bài 3:
Ví dụ: \(x^2\ge2x\) .
* Tại sao khi mà chia cả hai vế cho x thì chỉ nhân 1 trường hợp ( bị thiếu trường hợp). Còn khi mà chuyển vế sang cho lớn hơn hoặc bằng 0 thì lại đủ trường hợp. giải thích mình tại sao lại bị thiếu và đủ trường hợp ạ!
Giups mình đầy đủ chỗ (*) nhá!
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
Bài 2: ĐKXĐ luôn là thứ mà phải ghi ngay đầu bài làm để xác định được biểu thức có nghĩa. Tức là em ghi ĐKXĐ: $x+1\geq 0$ đầu tiên.
Sau đó mới giải ra $\sqrt{x+1}=1$

giải phương trình có chứa ẩn ở mẫu
Answer:
e) \(\frac{x-3}{x-2}-\frac{x-2}{x-4}=3\frac{1}{5}\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{16}{5}\)
\(\Leftrightarrow x^2-7x+12-x^2+4x-4=\frac{16}{5}.\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}.\left(x^2-6x+8\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}x^2-\frac{96}{5}x+\frac{128}{5}\)
\(\Leftrightarrow-\frac{16}{5}x^2+\frac{81}{5}x-\frac{88}{5}=0\)
\(\Leftrightarrow-\frac{16}{5}.\left(x^2-\frac{81}{16}x+\frac{11}{2}\right)=0\)
\(\Leftrightarrow x^2-\frac{81}{16}x+\frac{6561}{1024}-\frac{929}{1024}=0\)
\(\Leftrightarrow\left(x-\frac{81}{32}\right)^2=\frac{929}{1024}\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{81}{32}=\frac{\sqrt{929}}{32}\\x-\frac{81}{32}=-\frac{\sqrt{929}}{32}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{81+\sqrt{929}}{32}\\x=\frac{81-\sqrt{929}}{32}\end{cases}}}\)
f) \(\frac{x-3}{x-2}+\frac{x-2}{x-4}=-1\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)+\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{-\left(x-2\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2-4x-3x+12+x^2-4x+4=-x^2+4x+2x-8\)
\(\Leftrightarrow x^2+x^2+x^2-4x-3x-4x-4x-2x+12+4+8=0\)
\(\Leftrightarrow3x^2-9x-8x+24=0\)
\(\Leftrightarrow3x\left(x-3\right)-8\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\3x-8=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{8}{3}\end{cases}}}\)
Giải các phương trình chứa ẩn ở mẫu sau
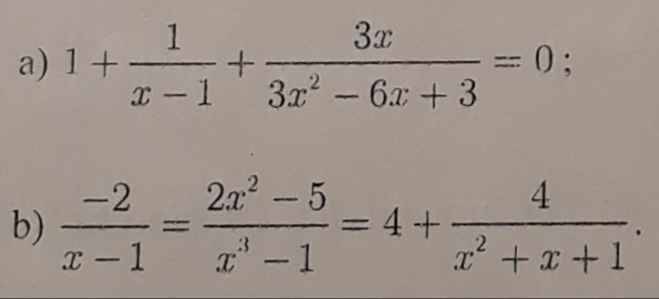
a: ĐKXĐ: x<>1
\(PT\Leftrightarrow1+\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)^2}=0\)
=>\(\dfrac{\left(x-1\right)^2+x-1+x}{\left(x-1\right)^2}=0\)
=>x^2-2x+1+2x-1=0
=>x^2=0
=>x=0
b: ĐKXĐ: x<>1
Đề sai rồi bạn, sao lại có hai dấu bằng kìa
Cho Na lần lượt vào rượu etylic, axit axetic, phenol. Trường hợp nào xảy ra phản ứng? Nếu thay bằng dung dịch NaOH, Na2CO3 thì kết quả như thế nào. Viết các phương trình phản ứng
- Cả 3 trường hợp đều xảy ra pư
+ \(2C_2H_5OH+2Na\rightarrow2C_2H_5ONa+H_2\)
+ \(2CH_3COOH+2Na\rightarrow2CH_3COONa+H_2\)
+ \(2C_6H_5OH+2Na\underrightarrow{t^o}2C_6H_5ONa+H_2\)
- Nếu thay bằng NaOH, chỉ có CH3COOH, C6H5OH pư
+ \(CH_3COOH+NaOH\rightarrow CH_3COONa+H_2O\)
+ \(C_6H_5OH+NaOH\rightarrow C_6H_5ONa+H_2O\)
- Nếu thay bằng Na2CO3, chỉ có CH3COOH pư
+ \(2CH_3COOH+Na_2CO_3\rightarrow2CH_3COONa+CO_2+H_2O\)
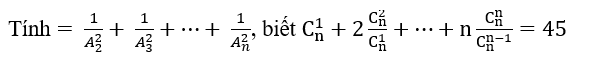
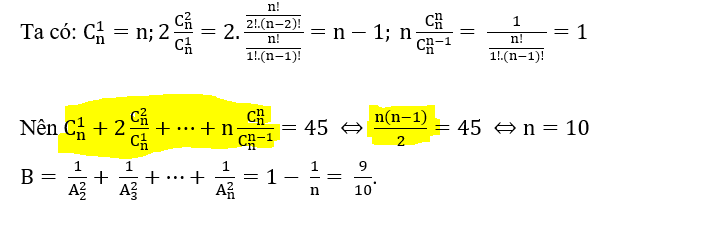
Cho em hỏi là em tính ra phần đánh dấu vàng dựa vào kết quả đã rút gọn ở trên nhưng lại không ra được kết quả tương đương bên cạnh ạ? Mình thế vào thì được n+n-1+...+1=45 thì làm thế nào để được như kết quả trên ạ.
Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)