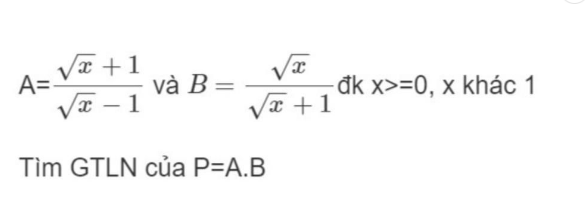Mọi người chỉ mình ạ!
Bài 1: giải phương trình
\(\sqrt{5x^2}=2x-1\)
* Chỉ mình tại sao bài này nếu mà bình phương 2 vế lên có giải được ra kết quả đúng không ạ. Giair thích rõ và chi tiết giúp mình nhé
* Với nhưng dạng thế nào thì có thể bình phương ạ!
Bài 2: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
* Với bài này mình chưa tìm điều kiện luôn mà giải ra thành \(\sqrt{x+1}=1\) rồi tìm điều kiện \(x+1\ge0\) cũng được ạ các bạn.
* Nó có phụ thuộc vào dạng bài không ạ hay là chỉ có những bài mới được làm như vậy còn chỉ có những bài thì phải tìm điều kiện ngay từ đầu ạ ( và làm như vậy có bị mất trường hợp nào đi không) . giải thích tại sao
Bài 3:
Ví dụ: \(x^2\ge2x\) .
* Tại sao khi mà chia cả hai vế cho x thì chỉ nhân 1 trường hợp ( bị thiếu trường hợp). Còn khi mà chuyển vế sang cho lớn hơn hoặc bằng 0 thì lại đủ trường hợp. giải thích mình tại sao lại bị thiếu và đủ trường hợp ạ!
Giups mình đầy đủ chỗ (*) nhá!
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
Bài 2: ĐKXĐ luôn là thứ mà phải ghi ngay đầu bài làm để xác định được biểu thức có nghĩa. Tức là em ghi ĐKXĐ: $x+1\geq 0$ đầu tiên.
Sau đó mới giải ra $\sqrt{x+1}=1$
Bài 2:
Ta có: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
\(\Leftrightarrow x+1=1\)
hay x=0
Bài 3: Muốn chia cả 2 vế cho $x$ thì $x\neq 0$ mới chia được. Do đó nó luôn bị thiếu TH $x=0$
Còn khi chuyển vế thì đưa nó về dạng $ab\geq 0$ thì đương nhiên ta xét được đầy đủ các TH dấu của nó rồi. Cái này hiển nhiên mà em?