Cho tam giác ABC vuông tại A , đường phân giác BD . Kẻ AE vuông góc BD , AE cắt BC ở K
a) CM : tam giác ABK cân tại B
b) CM : DK vuông góc BC
Vẽ hình vs giải dùm e vs ạ , e cần gấp
Cho tam giác ABC vuông tại A , đường phân giác BD . kẻ AE vuông góc BD ,
AE cắt BC ở K .
a, CM : tam giác ABK cân tại B
b, CM : DK vuông góc vs BC
c, KẺ AH vuông góc BC . CM : AK là tia Phân giác của Góc HAC
d, gọi I là giao điểm của AH và BD. Cm : IK song song AC
giúp mik nha
a) xét ABE vuông tại E và KBE vuông tại E
có góc ABE =KBE(gt)
BE chug
=> ABE=KBE ( ch -gn)
=> AB=KB( cạnh t/ư)
=> ABK cân tại B
b) xét ABD và KBD
có AB=KB
ABD=KBD
BD chung
=> ABD = KBD( cgc)
=> BAD = BKD
mà BAD = 90 độ
=> BKD =90 độ
hay DK vuông góc BC tại K
tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD, AAE cắt BC ở K
a) chứng minh tam ABK cân tại B
b) CM DK vuông góc BC
c) Kẻ AH vuông góc BC. CM: AK là phân giác của góc HAC
d) Gọi I là giao điểm của AH và BD. CM IK// AC
a) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
DBA=DBK hay EBA=EBA ( vì BD là phân giác của góc ABC)
=>\(\Delta ABE=\Delta KBE\) ( cạnh góc vuông- góc nhọn)
=>BA=BK
Vậy tam giác ABK cân tại B
b) Xét \(\Delta ABD\) và \(\Delta KBD\) có
AB=BK
ABD=KBD
Cạnh BD chung
=> \(\Delta ABD=\Delta KBD\left(c.g.c\right)\)
=> DKB=DAB=90 độ
Vậy \(DK⊥BC\)
c)d)
Xét \(\Delta ABI\) và \(\Delta KBI\) có
BA=BK
ABI=FBI
Cạnh BF chung
=> \(\Delta ABI=\Delta KBI\left(c.g.c\right)\)
=> IA=IK
Ta có DA=DK, IA=IK hay ID là đường trung trực của AK
=>AE=EK
Có \(DK⊥BC,AH⊥BC\) => DK//AH
=>DKE=EAI( 2 góc so le trong)
Xét tam giác vuông DKE và tam giác vuông EAI có
AE=EK
DKE=EAI
=> \(\Delta DKE=\Delta EAI\)(cạnh góc vuông- góc nhọn)
=>DK=AI
Mà DK=DA
=>AI=AD
Xét tam giác vuông DAE và tam giác vuông IAE có
DA=DI
Cạnh AE chung
=> \(\Delta DAE=\Delta IAE\)( cạnh huyền- cạnh góc vuông)
=>DAE=EAI hay góc CAK= góc KAH
Vậy AK là phân giác của HAC
Xét tam giác vuông IKE và tam giác vuông EAD có
AE=EK
KEI=AED( 2 góc đối đỉnh)
=>\(\Delta IKE=\Delta EAD\)( cạnh góc vuông- góc nhọn)
=>IKE=EAD
Mà IKE và EAD là 2 góc so le trong =>IK//AC
cho tam giác ABc vuông tại A, đường phân giác BD. kẻ AE vuông góc với BD, AE cắt BC ở K
a) biết ac= 8cm, ab = 6CM tính BC
b) tam giác ABK là tam giác gì
c) cM DK vuông góc BC
d kẻ AH vuông với BC, CM AK là phân giác của góc Hac
a) Có tam giác ABC vuông tại A
=>\(BC^2=AC^2+AB^2\) ( định lí Pitago)
=>\(BC^2=8^2+6^2=100\)
=> BC=10 (cm)
b) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
Góc DBA= góc DBK hay góc EBA= góc EBK ( vì BD là tia phân giác của góc ABC)
=> tam giác ABE= tam giác KBE( cạnh góc vuông- góc nhọn)
=> BA=BK ( 2 cạnh tương ứng)
Vạy tam giác ABK cân tại B
c) Nối D với K, ta có tam giác DKE vuông tại E
Theo câu b, ta có tam giác ABE= tam giác KBE
=> KE=EA( 2 cạnh tương ứng) và góc EAB=góc EKB (1)
Xét tam giác vuông DEA và tam giác vuông DEK có
Cạnh DE chung
EA=KE
=> tam giác DEA= tam giác DEK ( 2 cạnh góc vuông)
=> Góc DAE=góc DKE (2)
Từ (1) và (2) =>góc DKE+ góc EKB=góc DAE+ góc EAB= góc DAB=90 độ
=> Góc DKB= 90 độ
Vậy DK vuông góc với BC
d)
Có \(DK⊥BC,AH⊥BC\) =>DK//AB
=> góc DKE= góc EAH (1)
Có tam giác DEA=tam giác DEK
=> góc DAE= góc DKE (2)
Từ (1) và (2) => góc EAH= góc DAE hay góc CAK= góc KAH
Vậy AK là phân giác của góc HAC
Cho tam giác ABC vuông tại A . Vẽ đường phân giác BD (D thuộc AC ) .Kẻ AE vuông góc với BD (E thuộc BD) , đường thẳng AE cắt BC tại K . Chứng minh :
a) Tam giác BAK cân
b) DA = DK và DK vuông góc với BC
ban tu ve hinh
a) +) tam giac ABE co : ABE+BAE+BEA=180( dinh li tong 3 goc cua 1 tam giac)
ABE+BAE+90=180
ABE+BAE =180-90=90(1)
+) tam giac EBK co : EBK+KEB+BKE=180(dinh li tong 3 goc cua 1 tam giac )
EBK+90+BKE=180
EBK+BKE=90(2)
Vi ABE=EBK(BD la phan giac cua ABC) nen tu (1) va (2) suy ra BAE=BKE
suy ra tam giac BAK can tai B
b)Vi tam giac ABK can tai B nen AB=BK
xet tam giac ABD va tam giac KBD CO :
BD chung
ABD=KBD ( BD la phan giac cua ABC)
AB=AK(cmt)
NEN tam giac ABD= tam giaac KBD (c-g-c) nen AB=BK( 2 canh tuong ung ) ;BAD=BKD(2 goc tuong ung ) ma BAD=90 NEN DKB=90
SUY RA DK vuong goc voi BC
CAC GOC KO CO KI HIEU MU GOC BAN TU THEM VAO
a, xét tam giác ABE và tam giác KBE có : BE chung
góc ABE = góc KBE do BD là phân giác của góc BAC (gt)
góc AEB = góc KEB = 90 do ...
=> tam giác ABE = tam giác KBE (ch - gn)
=> BK = BA (đn)
=> tam giác BKA cân tại B (đn)
C tự vẽ hình nhé
a) Xét tg BEA và tg BEK có :
góc BEA = góc BEK = 90 độ ( AE vuông góc với BD)
góc ABE = góc KBE ( đường phân giác BD )
Cạnh BE chung
Do đó tg BEA = tg BEK (g.c.g)
=> BA = BK ( 2 cạnh t/ứng )
=> tg BAK cận tại B
b) Ta có ; tg BEA = tg BEK ( cmt )
=> AE = AK ( 2 cạnh t/ứng )
Xét tg DEA và tg DEK có
góc DEA = góc DEK = 90 độ (AE vuông góc với BD )
AE = AK ( cmt )
Cạnh BD chung
Do đó tg DEA = tg DEK (c.g.c)
=> DA = DK (2 cạnh t/ứng )
Xét tg BAD và tg BKD có:
góc ABD = góc KBD ( đường phân giác BD )
BA = BK (cmt)
Cạnh BD chung
Do đó tg BAD = tg BKD (c.g.c)
=> góc BAD = góc BKD ( 2 góc tương ứng )
Mà góc BAD = 90 độ ( tg ABC vuông tại A )
=> góc BKD = 90 độ
=> DK vuông góc với BC tại K
Bài 1: Cho tam giác ABC vuông tại A. Vẽ đường phân giác BD ( D thuộc AC ). Kẻ AE vuông góc BD ( E thuộc BD ). Đường thẳng AE cắt BC tại K.
a) CM: tam giác BAK cân.
b) Cho DC =10cm, KC = 8cm. Tính DK.
c) Vẽ tia Ax so cho AK là tia phân giác góc CAx, tia Ax cắt BD tại I. Chứng minh KI vuông góc AB.
Tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD, AE cắt BC ở K.
A) Chứng minh tam giác ABK cân tại B.
B) chứng minh DK vuông góc BC
C) kẻ AH vuông góc BC. Chứng minh AK là là tia phân giác của góc HAC.
D) Gọi I là giao điểm của AC và BD. Chứng minh AK//AC.
a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :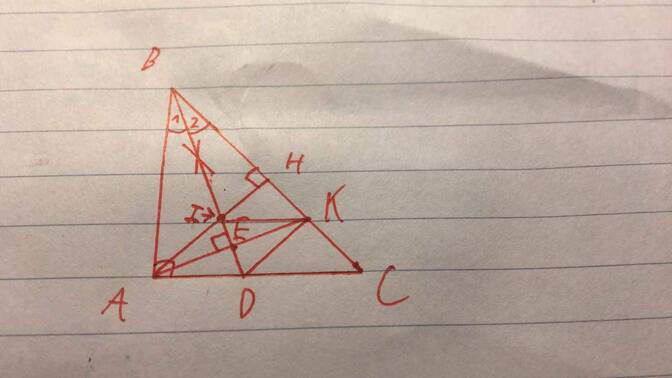
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAC
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAK
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
b ) Xét tam giác ABD và tam giác KBD , có
BD cạnh chung
góc ABD = góc KBD ( gt )
BA = BK ( tam giác ABK cân tại B )
suy ra tam giác ABD = tam giác KBD ( c.g.c)
suy ra góc BAD = góc BKD ( 2 góc tương ứng)
mà góc BAD = 90 độ
suy ra BKD = 90 độ
nên DK vuông góc BC