cho đa thức f(x)=x3 +(2m-n)x2-(m-3n)x+m.Tìm m và n để đa thức nhận m và n là nghiêm
Bài 10. Tìm m, n để đa thức \(f_{\left(x\right)}=\left(2m-n+1\right)x^2+m-3n+2\) là một đa thức không ?
- Để đa thức f(x) trên là một đa thức không thì :
\(\left\{{}\begin{matrix}2m-n+1=0\\m-3n+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-n=-1\\m-3n=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=-\dfrac{1}{5}\\n=\dfrac{3}{5}\end{matrix}\right.\)
Vậy ...
Cho các đa thức sau: M(x)=4x2+x3-2x+3-x-x3+3x-2x2; N(x)=x2-3+2x+3x3-x-3-3x2
a)Thu gọn và sắp sếp các đa thức trên theo lũy thừa giảm dần của biến.Cho biết hệ số tự do,hệ số cao nhất,bậc của mỗi đa thức.
b)Tính M(x)+N(x) và M(x)-N(x)
c)Chứng minh đa thức M(x) không có nghiệm
a: \(M\left(x\right)=2x^2+3\)
\(N\left(x\right)=3x^3-2x^2+x\)
b: \(M\left(x\right)+N\left(x\right)=3x^3+x+3\)
\(M\left(x\right)-N\left(x\right)=2x^2+3-3x^3+2x^2-x=-3x^3+2x^2-x+3\)
Câu c : M(x)=2x^2+3
ta có : x2 ≥ 0 với mọi x
=> 2x2 ≥ 0 => 2x2 + 3 ≥ 3 > 0=> M(x) ≠ 0 với mọi xVậy đa thức M(x) không có nghiệmCặp số (m;n) để đa thức Q(x)=m3 +(m-2)x2 -(3n-5)x-4n đồng thời chia hết cho x+1 và x-3 là
Sửa đê: Q=mx^3+(m-2)x^2-(3n-5)x-4n
\(\dfrac{Q\left(x\right)}{x+1}\)
\(=\dfrac{mx^3+mx^2-2x^2-2x+\left(2-3n+5\right)x-4n}{x+1}\)
\(=mx^2-2x+\dfrac{\left(7-3n\right)x+7-3n-7-n}{x+1}\)
\(=mx^2-2x+7-3n+\dfrac{-n-7}{x+1}\)
Q(x) chia hết cho x+1
=>-n-7=0
=>n=-7
=>Q(x)=mx^3+(m-2)x^2+26x-28
\(\dfrac{Q\left(x\right)}{x-3}=\dfrac{mx^3-3mx^2+\left(4m-2\right)x^2-3\left(4m-2\right)x+\left(12m-6+26\right)x-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+\dfrac{\left(12m+20\right)x-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+\dfrac{\left(12m+20\right)x-3\left(12m+20\right)+3\left(12m+20\right)-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+12m+20+\dfrac{36m+32}{x-3}\)
Q(x) chia hết cho x-3
=>36m+32=0
=>m=-8/9
Câu 16 Cho đa thức
M = x2 + 5x4 − 3x3 + x2 + 4x4 + 3x3 − x + 5
N = x − 5x3 − 2x2 − 8x4 + 4 x3 − x + 5
a. Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến
b. Tính M+N; M- N
Câu 17. Cho đa thức A = −2 xy 2 + 3xy + 5xy 2 + 5xy + 1
a. Thu gọn đa thức A.
b. Tính giá trị của A tại x= ![]() ;y=-1
;y=-1
Câu 18. Cho hai đa thức
P ( x) = 2x4 − 3x2 + x -2/3 và Q( x) = x4 − x3 + x2 +5/3
a. Tính M (x) = P( x) + Q( x)
b. Tính N ( x) = P( x) − Q( x) và tìm bậc của đa thức N ( x)
Câu 19. Cho hai đa thức: f(x) = 9 – x5 + 4x - 2x3 + x2 – 7x4
g(x) = x5 – 9 + 2x2 + 7x4 + 2x3 - 3x
a) Sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến
b) Tính tổng h(x) = f(x) + g(x).
c) Tìm nghiệm của đa thức h(x).
Câu 20: Cho P(x) = 2x3 – 2x – 5 ; Q(x) = –x3 + x2 + 1 – x.
Tính:
a. P(x) +Q(x);
b. P(x) − Q(x).
Câu 21: Cho đa thức f(x) = – 3x2 + x – 1 + x4 – x3– x2 + 3x4
g(x) = x4 + x2 – x3 + x – 5 + 5x3 – x2
a) Thu gọn và sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến. b) Tính: f(x) – g(x); f(x) + g(x)
c) Tính g(x) tại x = –1.
Câu 22: Cho đa thức P = 5x2 – 7y2 + y – 1; Q = x2 – 2y2
a) Tìm đa thức M = P – Q
b) Tính giá trị của M tại x=1/2 và y= -1/5
Câu 23 Tìm đa thức A biết A + (3x2 y − 2xy3 ) = 2x2 y − 4xy3
Câu 24 Cho P( x) = x4 − 5x + x2 + 1 và
Q( x) = 5x + 3 x2 + 5 + x2 + x4 .
a)Tìm M(x)=P(x)+Q(x)
b. Chứng tỏ M(x) không có nghiệm
Câu 25) Cho đa thức P(x) = 5x-![]() ; Q(x) = x2 – 9.; R(x) = 3x2 – 4x
; Q(x) = x2 – 9.; R(x) = 3x2 – 4x
a. Tính P(-1);Q(-3);R(![]() )
)
b. Tìm nghiệm của các đa thức trên
21:
a: \(f\left(x\right)=4x^4-x^3-4x^2+x-1\)
\(g\left(x\right)=x^4+4x^3+x-5\)
b: f(x)-g(x)
=4x^4-x^3-4x^2+x-1-x^4-4x^3-x+5
=3x^4-5x^3-4x^2+4
f(x)+g(x)
=4x^4-x^3-4x^2+x-1+x^4+4x^3+x-5
=5x^4+3x^3-4x^2+2x-6
c: g(-1)=1-4-1-5=-9
Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:
P ( x ) = m x 3 + ( m – 2 ) x 2 – ( 3 n – 5 ) x – 4 n
+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
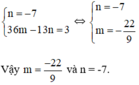
Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:
P(x) = mx3 + (m – 2)x2 – (3n – 5)x – 4n
+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
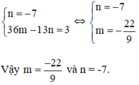
Cho 2 đâ thức P(x)=2x3-x+x2-x3+3x+5
Q(x)=3x3+4x2+3x-4x3-5x2+10
a thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến
b Tìm các đa thức M(x) Và N(x) biết rằng M(x)=P(x)+Q(x);N(x)=P(x)-Q(x)
\(a,P\left(x\right)=2x^3-x+x^2-x^3+3x+5\\ =\left(2x^3-x^3\right)+x^2+\left(-x+3x\right)+5\\ =x^3+x^2+2x+5\\ Q\left(x\right)=3x^3+4x^2+3x-4x^3-5x^2+10\\ =\left(3x^3-4x^3\right)+\left(4x^2-5x^2\right)+3x+10\\ =-x^3-x^2+3x+10\\ b,M\left(x\right)=P\left(x\right)+Q\left(x\right)=x^3+x^2+2x+5-x^3-x^2+3x+10\\ =\left(x^3-x^3\right)+\left(x^2-x^2\right)+\left(2x+3x\right)+\left(5+10\right)=5x+15\\ N\left(x\right)=P\left(x\right)-Q\left(x\right)=x^3+x^2+2x+5-\left(-x^3-x^2+3x+10\right)\\ =x^3+x^2+2x+5+x^3+x^2-3x-10\\ =\left(x^3+x^3\right)+\left(x^2+x^2\right)+\left(2x-3x\right)+\left(5-10\right)\\ =2x^3+2x^2-x-5\)
`a,P(x)= 2x^3 -x+x^2 -x^3 +3x+5`
`= (2x^3 -x^3)+x^2+(-x+3x) +5`
`= x^3 +x^2 + 2x+5`
`Q(x)=3x^3 +4x^2+3x-4x^3-5x^2+10`
`= (3x^3-4x^3)+(4x^2-5x^2)+3x+10`
`= -x^3 -x^2+3x+10`
`b,M(x)=P(x)+Q(x)`
`->M(x)=(x^3 +x^2 + 2x+5)+(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5+(-x^3) -x^2+3x+10`
`=(x^3 -x^3)+(x^2 -x^2)+(2x+3x)+(5+10)`
`= 5x+15`
`N(x)=P(x)-Q(x)`
`->N(x)=(x^3 +x^2 + 2x+5)-(-x^3 -x^2+3x+10)`
`=x^3 +x^2 + 2x+5-x^3 +x^2-3x-10`
`=(x^3-x^3)+(x^2+x^2)+(2x-3x)+(5-10)`
`=2x^2 -x-5`
Cho đa thức: f(x)=mx3 + (m-2)x^2 - (3n-5)x-4n
Hãy xác định m và n sao cho đa thức chia hết cho x+1 và x-3
\(f\left(x\right)⋮\left(x+1\right)\)tức là chia hết cho \(\left[x-\left(-1\right)\right]\)
Do đó: \(f\left(-1\right)=0\Rightarrow n=-7\)
Tương tự, \(f\left(x\right)⋮\left(x-3\right)\)nên \(f\left(3\right)=0\)
\(\Rightarrow36m-13n-3=0\)
Giải hệ\(\hept{\begin{cases}n=-7\\36m-13n-3=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n=-7\\m=\frac{-22}{9}\end{cases}}\)
Cho đa thức: f(x)= 3x4+9x3+7x+2 và g(x)=x+3
a) Thực hiện phép chia f(x) : g(x)
b) Tìm số nguyên âm x để f(x) chia hết cho g(x)
c) tìm m để đa thức k(x)= -x3-5x+2m chia hết cho g(x)
\(a,f\left(x\right):g\left(x\right)=\left(3x^4+9x^3+7x+2\right):\left(x+3\right)\\ =\left[3x^3\left(x+3\right)+7\left(x+3\right)-19\right]:\left(x+3\right)\\ =\left[\left(3x^3+7\right)\left(x+3\right)-19\right]:\left(x+3\right)\\ =3x^3+7.dư.19\)
\(c,\) Để \(k\left(x\right)⋮g\left(x\right)\Leftrightarrow-x^3-5x+2m=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\)
\(\Leftrightarrow-\left(-3\right)^3-5\left(-3\right)+2m=0\\ \Leftrightarrow27+15+2m=0\\ \Leftrightarrow2m=-42\\ \Leftrightarrow m=-21\)